Question 1076171: R0: 3,6,9,12,15,18,21,...
R1: 1,4,7,10,13,16,19,...
R2: 2,5,8,11,14,17,20,...
a) Write down an expression for the value of the general term in each of the three prgressions. Show that the integer 1706836 lies in R1. I got R0:3n, R1:3n-2 and R2:3n-1. Then i did 3n-2=1706836 and showed that n=568946, so it lies in R1 and is the 568946th term in the series.
b) Use the Binomial Theorem to show that if x is a term in R1 or R2 then x^6 is in R1. This is the part i don't know how to work out.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) I agree with your expressions for the the general term in each of the three sequences.
To show if any number belongs to one of them,
I would just add digits, using module 9 clock arithmetic. The number belongs in the sequence that contains the final sum.
If the ending sum is 0, 3, or 6, the number is divisible by 3, and belongs in R0.
If it is 1, 4, or 7, it belongs in R1; if 2,5, or 8, it belongs in R2.
For 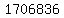 , ,
the final  part adds up to part adds up to 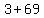 , and that 9 is dropped. , and that 9 is dropped.
The  and and  add up to add up to  , and that 9 is dropped. , and that 9 is dropped.
Then we are left with  , and since , and since  , we conclude that , we conclude that
when 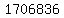 is divided by is divided by  , the remainder is , the remainder is  . .
So,  for some integer for some integer  , ,
and that shows that it belongs in R1.
HOW AND WHY CLOCK ARITHMETIC MOD 9 WORKS:
The sum of the digits of a number divisible by 9 is 9 or a multiple of 9.
As you are adding,
you drop partial sums that are 9, and keep adding the rest of the digits.
Similarly, for any partial two-digit sum,
you replace the sum of the digits for the two-digit partial sum.
At the end, you should have a one-digit final sum from 0 to 8.
b)The numbers in R1 and R2 are  away from a multiple of away from a multiple of  . .
We could write them all as 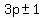 for some non-negative integer for some non-negative integer 
.
(If you - or your teacher - do not like that expression, you could use
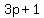 for terms of R1, with for terms of R1, with  , ,
and 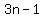 for terms of R2, for terms of R2,
and write twice as much for your proof).
For  , ,
  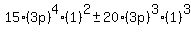  
 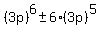  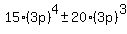  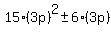 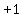
It should be obvious that all terms of that sum are multiples of  , ,
except that 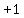 at the end, at the end,
and that shows that 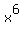 is a term in R1. is a term in R1.
If your teacher insisted on seeing the  that gives that gives 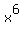 the right to belong to R1, the right to belong to R1,
you would have to write more, starting with getting out  as a common factor: as a common factor:
  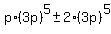     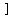 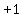 . .
|
|
|