Question 1076100: Please help me solve this by COMPLETING THE SQUARE
28x-2x^2=26
I got no real solution. This is what I did, please correct me.
-2x^2+28x=26
(28/2)^2=196
-2x^2+28x+196=26+196
since you cannot take the square root of a negative, i got no real solution
√-2x^2 = no real solutions
Please help me, I am very confused. Thank you in advance, Emily
Found 4 solutions by Alan3354, josgarithmetic, MathLover1, MathTherapy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! -2x^2+28x=26
(28/2)^2=196 **** Should be (b/2a)^2 = 49
-2x^2+28x+196=26+196
since you cannot take the square root of a negative, i got no real solution
√-2x^2 = no real solutions
=================
-2x^2+28x=26
I would start with this:
Divide by -2
x^2 - 14x = -13
Make it easier.
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please help me solve this by COMPLETING THE SQUARE
28x-2x^2=26
I got no real solution. This is what I did, please correct me.
-2x^2+28x=26
(28/2)^2=196
-2x^2+28x+196=26+196
since you cannot take the square root of a negative, i got no real solution
√-2x^2 = no real solutions
Please help me, I am very confused. Thank you in advance, Emily
First of all, you're INCORRECT. You should see that after FACTORING OUT a GCF, 2, you'll end up with  . .
This can be FACTORED to get roots/solutions/zeroes of x = 13, or x = 1.
From this, it's clear that these will be your solutions, and they are REAL.
You could have also used the DISCRIMINANT to see if it really has No real solutions. If you did. You'd see that it does have 2 REAL solutions.
Now that we know this, let's get to the solutions by COMPLETING the SQUARE.


 ------- Rearranging equation ------- Rearranging equation
 -------- Taking -------- Taking 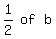 , squaring it, and adding the result to both sides , squaring it, and adding the result to both sides



 ------ Taking the square root of both sides ------ Taking the square root of both sides
 ======> ======> 

|
|
|