SOLUTION: the length of a rectangular plot of land with an area of 880 meters is 24 meters more than its width. If w represents the width of the plot of land in meters, write an equation in

Click here to see ALL problems on Geometry Word Problems

Question 1075902: the length of a rectangular plot of land with an area of 880 meters is 24 meters more than its width. If w represents the width of the plot of land in meters, write an equation in the form x^2+bx+c=0 that will be used to find the possible values if the width of the land
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617) (Show Source):
You can put this solution on YOUR website!
Length is w+24 and width is w.
Area given as 880.

Answer by ikleyn(52786) (Show Source):
You can put this solution on YOUR website!
.
There is the way to solve the problem MENTALLY.

Let "x" be the value of the mid-point between L and W: x = w + 12. Then the width W = x - 12, while the length is L = x + 12. WL = 880 then becomes (x-12)*(x+12) = 880, or x^2 - 144 = 880. Then x^2 = 880 + 144 = 1024, and x = 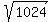= 32. Therefore, W = 32 - 12 = 20 and L = 32 + 12 = 44. Answer. The dimensions of the rectangle are 44 m and 20 m.