Question 1075739: there are 3 positive whole numbers, the product of first and second number is 24, second and third number is 48, first and third number is 32. find the value of three number?
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! x,y,z are numbers
xy=24
yz=48
xz=32
x=(24/y)
(24/y)*z=32
yz=48, so z=(48/y)
(24/y)(48/y)=32
(1152/y^2)=32
32y^2=1152
y^2=36
y=6
x=4
z=8
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
there are 3 positive whole numbers, the product of first and second number is 24, second and third number is 48,
first and third number is 32. find the value of three number?
~~~~~~~~~~~~~~~~
There is much more elegant solution:
xy = 24, (1)
yz = 48, (2)
xz = 32. (3)
Multiply all three equations (both sides). You will get
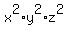 = 24*48*32, or
xyz = +/- = 24*48*32, or
xyz = +/- 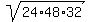 , or
xyz = +/- , or
xyz = +/- 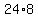 = +/- 192. (4)
Now divide equation (4) by the equation (1) (both sides). You will get
z = +/- 8.
Next divide equation (4) by the equation (2) (both sides). You will get
x = +/- 4.
Finally, divide equation (4) by the equation (3) (both sides). You will get
y = +/- 6
Answer. There are TWO solutions: a) (x,y,z) = (4,6,8), and b) (x,y,z) = (-4,-6,-8).
If you want the solution in positive numbers, then keep a). = +/- 192. (4)
Now divide equation (4) by the equation (1) (both sides). You will get
z = +/- 8.
Next divide equation (4) by the equation (2) (both sides). You will get
x = +/- 4.
Finally, divide equation (4) by the equation (3) (both sides). You will get
y = +/- 6
Answer. There are TWO solutions: a) (x,y,z) = (4,6,8), and b) (x,y,z) = (-4,-6,-8).
If you want the solution in positive numbers, then keep a).
Solved.
Lesson to learn from this solution: This problem was designed with the only SPECIAL goal: in order for you learn THIS solution.
|
|
|