Question 1075322: Simplify and state restrictions
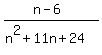  
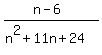  
Found 2 solutions by Boreal, Edwin McCravy:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! (n-6)/(n+8)(n+3)*(n+3)/(n+1), invert when you divide and multiply
the (n+3) cancel
(n-6)/(n+8)(n+1)
This does not exist at x=-8, -3 or -1, the last because you would be dividing by 0.
Answer by Edwin McCravy(20062)   (Show Source): (Show Source):
You can put this solution on YOUR website! Simplify and state restrictions
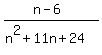  
We factor the denominator on the first fraction:
   None of the denominators can be 0, so
we must restrict the denominators
n+8≠0, n+3≠0
n≠-8, n≠-3
However we must not divide by 0, so the numerator
of what we are dividing by must not equal 0 either
So the numerator of the second fraction also cannot
be 0, for then the fraction that we are dividing by
would be 0, and we cannot divide by zero.
n+1≠0
n≠-1
So the restrictions are n≠-8, n≠-3, and n≠-1
To finish the problem, we invert the second fraction
and multiply:
None of the denominators can be 0, so
we must restrict the denominators
n+8≠0, n+3≠0
n≠-8, n≠-3
However we must not divide by 0, so the numerator
of what we are dividing by must not equal 0 either
So the numerator of the second fraction also cannot
be 0, for then the fraction that we are dividing by
would be 0, and we cannot divide by zero.
n+1≠0
n≠-1
So the restrictions are n≠-8, n≠-3, and n≠-1
To finish the problem, we invert the second fraction
and multiply:
   and cancel:
and cancel:
  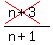
  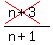
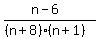 , n≠-8, n≠-3, n≠-1
Edwin , n≠-8, n≠-3, n≠-1
Edwin
|
|
|