This is a binomial experiment.
We calculate the mean:
 That's the expected number of 1's.
[Expected number, is really the expected AVERAGE number. I.e.,
if you rolled the die 8 times each day for a year, and averaged
up how many 1's you got each day, you would expect to get an
average of about 1.333... 1's per day.]
We calculate the standard deviation
That's the expected number of 1's.
[Expected number, is really the expected AVERAGE number. I.e.,
if you rolled the die 8 times each day for a year, and averaged
up how many 1's you got each day, you would expect to get an
average of about 1.333... 1's per day.]
We calculate the standard deviation
 2 standard deviations is
2 standard deviations is  2 standard deviations below the expected number is
2 standard deviations below the expected number is


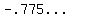 2 standard deviations above the expected number is
2 standard deviations above the expected number is


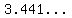 To get the number of 1's to be between those, we must roll
either 0, 1, 2, or 3 1's
We do that with a TI-83 or TI-84 calculator.
press 2ND then VARS
use down arrow to scroll down to binomcdf(
[Warning! Don't scroll to binompdf( by mistake!!!]
press ENTER
depending on how new or old your calculator is,
1. If you see the "wizard", make the wizard read
binomcdf
trials:8
p:1/6
x value:3
Paste
scroll to "Paste" and press ENTER
you will see binomcdf(8,1/6,3)
2. Or if you have an older model,
you just see binomcdf(, make it read binomcdf(8,1/6,3)
press ENTER
See: .9693435881
That's the probability of rolling 0,1,2,or 3 1's, which is a number of
1's between 2 standard deviations below the expected number and 2
standard deviations above the expected number.
Edwin
To get the number of 1's to be between those, we must roll
either 0, 1, 2, or 3 1's
We do that with a TI-83 or TI-84 calculator.
press 2ND then VARS
use down arrow to scroll down to binomcdf(
[Warning! Don't scroll to binompdf( by mistake!!!]
press ENTER
depending on how new or old your calculator is,
1. If you see the "wizard", make the wizard read
binomcdf
trials:8
p:1/6
x value:3
Paste
scroll to "Paste" and press ENTER
you will see binomcdf(8,1/6,3)
2. Or if you have an older model,
you just see binomcdf(, make it read binomcdf(8,1/6,3)
press ENTER
See: .9693435881
That's the probability of rolling 0,1,2,or 3 1's, which is a number of
1's between 2 standard deviations below the expected number and 2
standard deviations above the expected number.
Edwin