Question 1075086: Give the side length of a triangle to the nearest tenth and angle measures to the nearest degree
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! What is your triangle like?
To calculate the length of a side and measure of an angle of a triangle
you need to know something about that triangle.
If you have a specific triangle problem in mind, post that problem.
Right triangles are the easiest cases.
Of course the have one right angle, measuring  . .
The other two angles are acute angles (smaller than a right angle).
Since the measures of the 3 angles in any triangle
always add up to  , ,
if you have a right triangle and the measure,  , ,
of one of the acute angles,
it is easy to find the measure of the other acute angle as
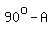 . .
If you are given the lengths of 2 sides of a right triangle,
you can find the length of the other side,
and the measures of all the angles.
Triangles that do not have a right angle are a little trickier.
If you have the measure of one angle,
and the length of the side opposite that angle,
you need just one more piece of information
to find everything about that triangle.
To do that you start by applying Law of sines.
Calculations are not too difficult,
but you need to understand hoW to use
trigonometric functions
If you do not have the measure of one angle,
and the length of the side opposite that angle,
you still need at least pieces of information,
and calculations will be more complicated.
You will need to use Law of cosines
|
|
|