|
Question 1074902: Find the foci of the ellipse whose major axis has endpoints $(0,0)$ and $(13,0)$ and whose minor axis has length 12.
Enter your answer as a list of pairs separated by commas.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The center of that ellipse is the midpoint of the major axis,
half way between (0,0) and (13,0) on line y=0.
The coordinates of that midpoint are the averages of the coordinates of the vertices.
The midpoint is (6.5,0) , and that is the center of the ellipse.
The distance from the center to each vertex is called the semi-major axis and represented as  . .
In this case  . .
Half of the minor axis is called the semi-minor axis and is represented with  . .
That is the distance from the center to each co-vertex.
In this case  . .
The distance from the center to each focus is represented with  , ,
and is related to  and and  by by  . .
In this case  . .
Solving for  : :

A calculator can do that, but I don't need one




 . .
That is the distance from center (6.5,0) to each focus.
The foci are on the same line as the vertices, line y=0,
on either side of the center,
so the x-coordinate of one focus is  , ,
and the x-coordinate of the other focus is  . .
So, the foci are 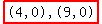 . .
|
|
|
| |