Question 1074727: The admissions office at a Big State University needs to decide how many in state and how many out-of-state students to admit to the next class. Like many universities, Big State University has limited resources, and budget considerations have to play a part in the admissions policy. (Let X = the number of in-state students and Y = the number of out-of-state students)
Here are the constraints;
A ). The college president wants this class to contribute a total of at least $2,520,000 to the school after it graduates. In the past, BSU has gotten an average of $8000 in contributions from each in-state student and an average of $2000 from each out-of-state student admitted.
B). The facility is requiring that the school admit at least as many out-of-state students as in-state students.
C). The housing office is not able to spend more than $84,000 to cover costs such as meals and utilities for students in dormitories during vacation periods. In-state students will cost the office an average of $100 each vacation time expenses and out-of-state students will cost an average of $200 each.
The college treasurer needs to minimize costs. It costs an average of $7200 a year to teach an in-state student and an average of $6000 a year to teach an out-of-state student.
Your task is to recommend how many students from each category should be admitted into BSU in order to minimize the educational costs.
This is one of the challenge questions on my College algebra homework. I have asked a few of my friends to help me figure it out but none of them seem to know how to solve it. I would greatly appreciate it if someone could walk me through the steps so I can also teach my classmates how to solve it. Thanks!
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this looks like a linear engineering type problem.
it can be solved graphically.
your solution will be that the cost is minimized when 252 in state and 252 out of state students are admitted.
all the constraints are met as you will soon see.
let x equal the number of in state students.
let y equal the number of out of state students.
your objective function is to minimize costs.
your objective function is therefore cost = 7200x + 6000y
that's an average of 7200 a year to teach one in state student and 6000 a year to teach an out of state student.
your constraint functions are as follows:
constraint function 1 is 8000x + 2000y >= 2,520,000
this means that each in state student contributes an average of 8000 to the school after that student graduates and each out of state student contributes an average of 2000 to the school after that student graduates.
the total contribution the school requires is 2,520,000.
the number of students admitted should be able to contribute at least that much after they graduate.
constraint functions 2 and 3 are:
x >= 0
y >= 0
this means that the number of in state students can't be negative and the number of out of state students can't be negative.
constraint function 4 is y >= x
this means that the number of out of state students must be greater than or equal to the number of in state students.
constraint function 5 is 100x + 200y <= 84,000
this means that the cost for each in state student and the cost for each out of state student during vacation time periods must not be greater than 84,000.
each in state student costs an average of 100 dollars and each out of state student costs an average of 200 dollars during vacation time periods.
i believe that's all of them.
in summary.
your objective function is:
cost = 7200x + 6000y
your constraint functions are:
x >= 0
y >= 0
y >= x
8000x + 2000y >= 2,520,000
100x + 200y <= 84,000
solve for y in those functions that can be solved for y and you get:
x >= 0
y >= 0
y >= 0
y >= 1260 - 4x
y <= 420 - x/2
you would graph the equality portion of the constraint functions and then find the areas on the graph that satisfies the inequality portion of the functions.
that will be your feasible region.
you then find the corner points of the feasible region and evaluate your objective function at those corner points.
your minimum cost will be at one of those corner points.
the equations that you will graph are:
x = 0
y = 0
x = y
y = 1260 - 4x
y = 420 - x/2
graph those equations and find the area of the graph that satisfies the inequalities and you will get something that looks like this:
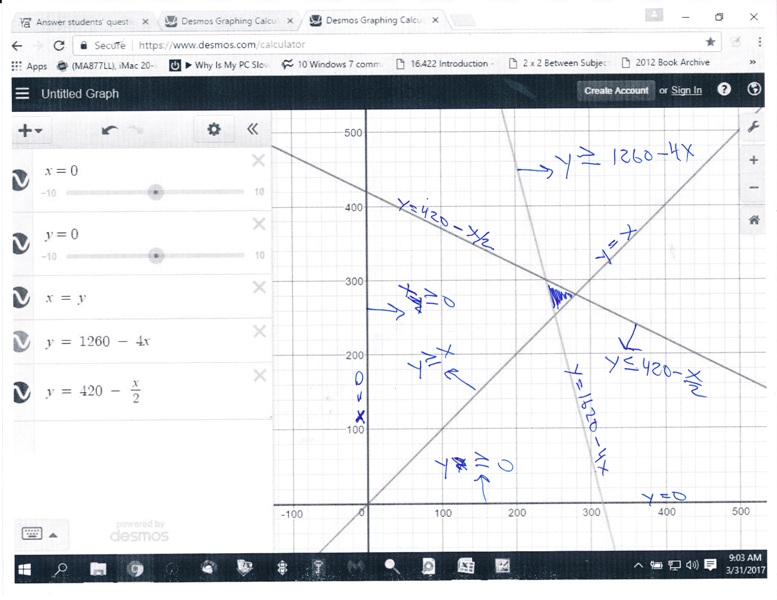
a close up of the region of feasibility with the corner points identified is shown below:
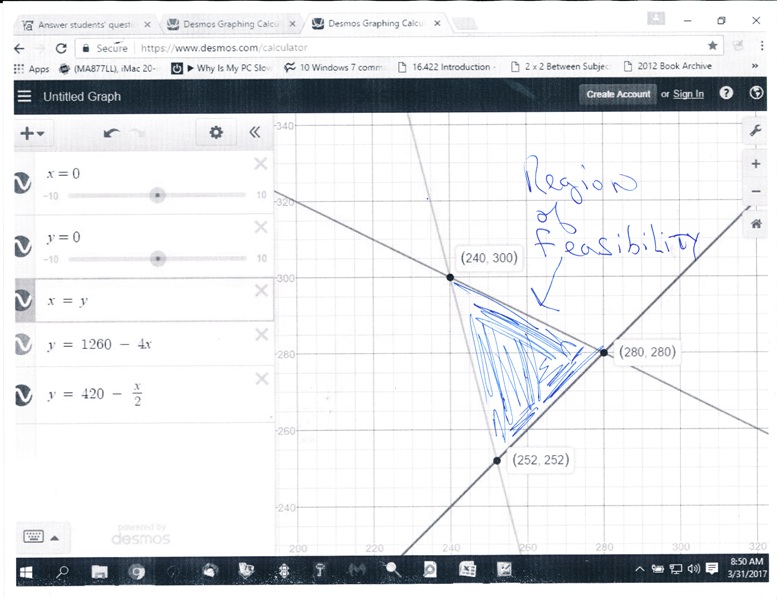
when you evaluate the objective function at each of these corner points, you will find that the minimum cost is when x = 252 and y = 252.
all the constraints are satisfied at that corner point.
they should admit 252 in state and 252 out of state students to minimize costs and satisfy all their constraints.
the calculations to find the minimum costs are:
x y 7200x + 6000y
240 300 7200 * 240 + 6000 * 300 = 3,528,000
252 252 7200 * 252 + 6000 * 252 = 3,216,400
280 280 7200 * 280 + 6000 * 280 = 3,696,000
you can see that the minimim cost is achieved when x and y are both equal to 252.
the constraint functions have to be satisfied when x = 252 and y = 252.
go back to the original constraint functions and see if they are satisfied.
x >= 0 and y >= 0 are satisfied because x and y are greater than 0.
y >= x is satisfied because 252 is greater than or equal to 252.
8000x + 2000y >= 2,520,000 is satisfied because 8000 * 252 + 2000 * 252 is equal to 2,520,000 which is greater than or equal to 2,520,000.
100x + 200y <= 84,000 is satisfied because 100 * 252 + 200 * 252 is equal to 75,600 which is smaller than or equal to 84,000.
|
|
|