Question 1074625: Find all positive integers $n$ for which $n^2 - 19n + 99$ is a perfect square.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! TIP:
When I see $ wrapping equations,
it remind me of LATEX,
and makes me suspect you come from artofproblemsolving.
We use triple curly brackets, like {, here.
I am going to look at the embarrassingly simpler solution in that website
as soon as I finish typing my awkward solution here.
ONE WAY:
We want  to be true to be true
for some positive integers  and and  . .








Let me abbreviate with the change of variables
 , ,
knowing that  is a positive, even integer, is a positive, even integer,
and  is an integer. is an integer.
The equation becomes
 , so much easier to write, , so much easier to write,
and immediately we think of
 . .
Are those factors in brackets positive or negative?
We knew that  , ,
so 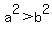 --> --> 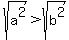 --> --> 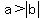 , ,
so whether 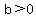 or or  , ,
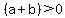 and and 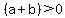 . .
Back to the product of positive integer factors
 . .
The factors could be 1 and 35 or 5 and 7.
We have 4 possibilities:
 --> --> --> --> --> -->
 --> --> --> --> --> -->
 --> --> --> --> --> -->
 --> --> --> --> --> -->
ANOTHER WAY:
 <--> <--> , so if , so if  , ,
 --> --> --> --> . .
The two perfect squares we look for, 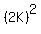 and and 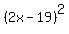 , ,
cannot be too large if their difference is only  . .
There are not many possible solutions,
and they will all be close to the  of the vertex. of the vertex.
So, listing values for  around around  , ,
(or listing values for 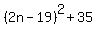 for for  around around  ), ),
until you find a perfect square is an option.
PS: Actually, it was not that the artofproblemsolving solution was so much simpler,
but that they skip steps/explanations that "should be obvious,"
so they do not need to write as much.
If you get all those steps, artofproblemsolving is a fun site,
but I tend to/like to overexplain, so I belong at this website.
|
|
|