Question 1074607: The pool has 3 pipes, A,B and C. Pipes A and B can fill the pool in 14 hours, pipes A and C can fill it in 16 hours, and pipes B and C can fill it in 20 hours. How long will it take to fill the pool if all 3 pipes are turned on?
A little confused to set this up. Can someone help me?
Thank you.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Consider the speed/rate with which the pipes can fill the pool,
in pool-fuls per hour.
For example, if a pipe can fill the pool in 10 hours,
its flow rate or pool-filling speed is  pool-fuls per hour.
So, if the rates of A, B, and C are  ,  , and  respectively,
the rates add up to give you
 ,  , and  .
All 3 equations together for a system of linear equations that you could solve.
Once you knew , , and ,
calculate 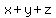 , the rate for the 3 pipes together,
and from there calculate  ,
the time to fill the pool with all 3 pipes.
However, adding up the 3 equations, you get
 <--->  <---> 
and the time needed to fill the pool using all 3 pipes at once is
   hours.
That is about 10 hours, 52 minutes, 26 seconds.
(The exact calculation cones to
10 hours, 52 minutes, 25 and 65/103 seconds.
|
|
|
