Question 1074418: I have some dimes, nickels, and quarters. There are 18 coins in all. The total number of dimes and nickels is equal to the number of quarters. The value of coins is $2.85. How many of each coin so I have?
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39630)   (Show Source):
Answer by ikleyn(52884)  (Show Source):
You can put this solution on YOUR website! .
The very first conclusion from the condition is this: The number of quarters is 9 (=  ).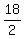
Then the problem is easily reduced to only TWO unknowns.
There are 9 coins, dimes and nickels. The value of coins is 285-9*25 = 60 cents. How many of each of the two nominations?
----> 3 dimes and 6 nickels.
Answer. 6 nickels, 3 dimes and 9 quarters.
This problem is for mental solution.
Answer by MathTherapy(10556)  (Show Source):
You can put this solution on YOUR website! I have some dimes, nickels, and quarters. There are 18 coins in all. The total number of dimes and nickels is equal to the number of quarters. The value of coins is $2.85. How many of each coin so I have?
Don't even look at the other person's attempt as, besides confusing you, he is trying to have you spend as much time as possible solving this problem
By doing the following you will quickly determine the number of quarters
Let the number of dimes, nickels, and quarters be N, D, and Q, respectively
Then we get: N + D + Q = 18 ------- eq (i)
Also, D + N = Q ------- eq (ii)
And, .1D + .05N + .25Q = 2.85 ------- eq (iii)
Q + Q = 18 ------- Substituting Q for D + N in eq (i)
2Q = 18
Q, or number of quarters = 
D + N = 9______D = 9 - N ------- Substituting 9 for Q in eq (ii) ------- eq (iv)
.1D + .05N + .25(9) = 2.85 ------- Substituting 9 for Q in eq (ii)
.1D + .05N = .6 ------- eq (v)
.1(9 - N) + .05N = .6 ------- Substituting 9 - N for D in eq (v)
.9 - .1N + .05N = .6
- .1N + .05N = .6 - .9
- .05N = - .3
N, or number of nickels = 
D = 9 - 6 ------- Substituting 6 for N in eq (iv)
D, or number of dimes = 
|
|
|
