You can
put this solution on YOUR website! .
Let "r" be the speed at the first part of the trip, in km/h.
Then the speed at the second part is (r-7) km/h.
The "time" equation is
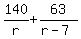 = 3.
Solve it for "r". For it, multiply both sides of the equation by r*(r-7). You will get
140*(r-7) + 63r = 3r*(r-7).
Simplify and solve this quadratic equation.
= 3.
Solve it for "r". For it, multiply both sides of the equation by r*(r-7). You will get
140*(r-7) + 63r = 3r*(r-7).
Simplify and solve this quadratic equation.