SOLUTION: The volume of a box is 2p^4 + 14p^3 + 20p^2. The height is p and the width is p + 5. What is the length?

Algebra ->  Volume -> SOLUTION: The volume of a box is 2p^4 + 14p^3 + 20p^2. The height is p and the width is p + 5. What is the length?      Log On


   

Question 107379: The volume of a box is 2p^4 + 14p^3 + 20p^2. The height is p and the width is p + 5. What is the length?
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
The volume of any rectangular solid is given by 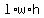l%2Aw%2Ah, which means that if you know the volume and two of the dimensions, you can find the third dimension by dividing the volume by one of the given dimensions and then dividing that quotient by the other given dimension.
We know that v+=+2p%5E4+%2B+14p%5E3+%2B+20p%5E2, and

we know that h=p and w+=+p%2B5

First, divide the volume expression by p, leaving:

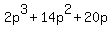
2p%5E3+%2B+14p%5E2+%2B+20p

Then divide by p + 5, the other given dimension:

Separate the middle term into two terms, 14p%5E2=10p%5E2%2B4p%5E2 giving:

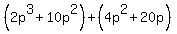%282p%5E3+%2B+10p%5E2%29%2B%284p%5E2+%2B+20p%29.

Then divide each set of two terms by p+5, thus:

%282p%5E3+%2B+10p%5E2%29%2F%28p%2B5%29=2p%5E2, and

%284p%5E2+%2B+20%5Ep%29%2F%28p%2B5%29=4p.

Adding those two results gives you the length: 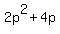2p%5E2+%2B+4p

To check the work, multiply the length that we just determined times the width and the height. We should arrive at the original volume expression.

%282p%5E2+%2B+4p%29%28p%2B5%29=2p%5E3%2B4p%5E2%2B10p%5E2%2B20p=2p%5E3%2B14p%5E2%2B20p
%282p%5E3%2B14p%5E2%2B20p%29p=2p%5E4+%2B+14p%5E3+%2B+20p%5E2, which was the original volume expression. Check!