Question 1073654: please help me Find the center, vertices, foci and endpoints with the minor axis of the ellipse of 2x^2+3y^2=18
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
please help me Find the center, vertices, foci and endpoints with the minor axis of the ellipse of 2x^2+3y^2=18
~~~~~~~~~~~~~~~~~~~~~~~
2x^2+3y^2 = 18 ---> (divide both sides by 18. You will get) --->
 = 1 ---> = 1 --->
 = 1.
It is the canonical equation of the ellipse with the center at the origin (x,y) = (0,0),
the major semi-axis a = 3, the minor semi-axis b = = 1.
It is the canonical equation of the ellipse with the center at the origin (x,y) = (0,0),
the major semi-axis a = 3, the minor semi-axis b =  .
Vertices are (3,0), (-3,0), ( .
Vertices are (3,0), (-3,0), ( , ,  ), ( ), ( , ,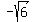 ),
The linear eccentricity of the ellipse is the number ),
The linear eccentricity of the ellipse is the number  = = 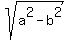 = =  = =  .
The foci are the points (c,0) = ( .
The foci are the points (c,0) = ( , , ) and (-c,0) = ( ) and (-c,0) = ( , , ). ).

Figure. The ellipse  = 1. = 1.
See the lessons
- Ellipse definition, canonical equation, characteristic points and elements
- Identify the vertices, co-vertices and foci of the ellipse given by an equation
- Find a standard equation of an ellipse given by its elements
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"Conic sections: Ellipses. Definition, major elements and properties. Solved problems".
|
|
|