SOLUTION: Flying with the wind, a small plane flew 240 mi in 2 h. Against the wind, the plane could fly only 210 mi in the same amount of time. Find the rate of the plane in calm air and the

Let "u" be the speed of the plane at no wind (=same as in calm air), in mph.
Let "v" be the speed of wind.

Then the effective speed of the plane flying WITH the wind is (u+v) mph (relative to the ground).

the effective speed of the plane flying AGAINST the wind is (u-v) mph (relative to the ground).

According to the condition, 
the plane effective speed is  = 120 mph flying  with    the wind,
and       effective speed is 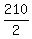 = 105 mph flying  against the wind.

It gives you two equations 

u + v = 120,    (1)
u - v = 105.    (2)

Add the two equations (both sides). You will get

2u = 120 + 105 = 225.   Hence,  u = 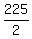 = 112.5.

Thus the speed of the plane at no wind is 112.5 mph.

Next, from the equation (1) v = 120 - u = 120 - 112.5 = 7.5 mph.

Thus the speed of the wind  is 7.5 mph.

Answer.  The speed of the plane at no wind is 112.5 mph..

         The speed of the wind  is 7.5 mph.

Check.  The speed of the plane with the wind is 112.5 + 7.5 = 120 mph, and the flight time is  = 2 hours.

        The speed of the plane against the wind is 112.5 - 7.5 = 105 mph, and the flight time is  = 2 hours.

        Checks !