SOLUTION: z-|z|=8+4i Find all complex numbers z that satisfy the equation:

Let z = a + bi be our complex number under the question.
We need to find its real and imaginary parts "a" and "b".

As you, probably, know  |z| = .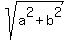

So, the given equation becomes

a + bi - 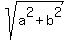 = 8 + 4i.


It actually deploys in two independent equations for the real part and the imaginary part separately:

a - 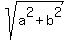 = 8     (1)     and
b            = 4.    (2)

Equation (1) is equivalent to

a - 8 = ,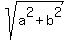

 = ,

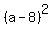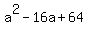 = ,    (I substituted b= 4)

-16a + 64 = 16  --->  -16a = 16-64  --->  -16a = -48  ---> a = 3.


So, the logic leads us to the solution  a = 3, b = 4, i.e. z = 3 + 4i.


Now CHECK this solution: 3 + 4i -  = 3 + 4i - 5 = -2 + 4i.


It doesn't check !!!


The conclusion is: The given equation HAS NO solutions.

let z = x + yi, where x and y are real

Substitute in





Set real parts equal, and imaginary parts equal:

,  
                   

Substitute y=4







Square both sides:



Cancel the x2's







But we must check to see if 3 is 
a solution or only an extraneous answer.
Substitute in:








That's false so 3 is extraneous and there
is no solution.

Edwin