SOLUTION: There are 10 points A,B... In a plane no three on the same line 1)how many lines are determined by the points? 2)how many of these lines do not pass through A or B ? 3)how ma

Algebra ->  Permutations -> SOLUTION: There are 10 points A,B... In a plane no three on the same line 1)how many lines are determined by the points? 2)how many of these lines do not pass through A or B ? 3)how ma      Log On


   

Question 1073434: There are 10 points A,B... In a plane no three on the same line
1)how many lines are determined by the points?
2)how many of these lines do not pass through A or B ?
3)how many triangle are determined by the points ?
4)how many of these triangles contain the point A ?
5) how many of these triangles contain in side AB ?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
1) There are 10-1=9 A-->X rays connecting point A to the other 9 points.
There are also 9 rays originating in each of the other points.
There is a total of 9%2A10=90 rays.
However, each pair of points, accounting for 2 rays, determines only 1 line.
The number of lines associated with the 90 possible rays is
90%2F2=highlight%2845%29 .

2) That would be the number of lines that can be made with the other 8 points.
Using the same reasoning used for part 1, we can calculate it as
8%2A7%2F2=4%2A7=highlight%2828%29 .
Another way to the answer:
There are 8 rays originating in point A that do not pass through B.
There are 8 rays originating in point B that do not pass through A.
Altogether, that adds to 8%2B8=16 rays (and lines) connecting A or B
with another point,
and none of those lines is counted twice.
Then there is 1 more line, passing through A and B: line AB.
So, there is a total of 8%2B8%2B1=17 lines passing through A and/or B.
The remaining 45-17=highlight%2828%29 lines .

3) That is how many sets of 3 points we can pick out of that set of 10 points.
Using what was taught in math class about combinations, we can calculate that number as
.
A fifth-grader could also decide that there would be
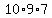10%2A9%2A7 possible 3-letter sequences,
but that each triangle could have its vertices listed as
6 different sequences (such as ABC, ACB, BAC, BCA, CAB, and CBA), meaning that the number of triangles is
10%2A9%2A8%2F6=720%2F6=highlight%28120%29 .

4) The number of triangles that contain the point A
is the number of pairs (sets of 2 items, not ordered lists of 2 items)
that can be made from the other 10-1=9 letters.
That is matrix%282%2C1%2C9%2C2%29=9%21%2F%282%21%2A7%21%29=9%2A8%2F2=9%2A4=highlight%2836%29 .

5) The number of triangles that contain side AB
is the number of points available to become the third vertex:
10-2=highlight%288%29 .
That part is easy enough for a 3-year old,
but it may be difficult if you have been conditioned to think
that you need help from formal education to answer every question.