Question 1073431: What is present value of annuity of 2300 payable at the end of each 8 months for 5 years if money is worth 4% compounded semiannually
Answer by Theo(13342)   (Show Source): (Show Source):
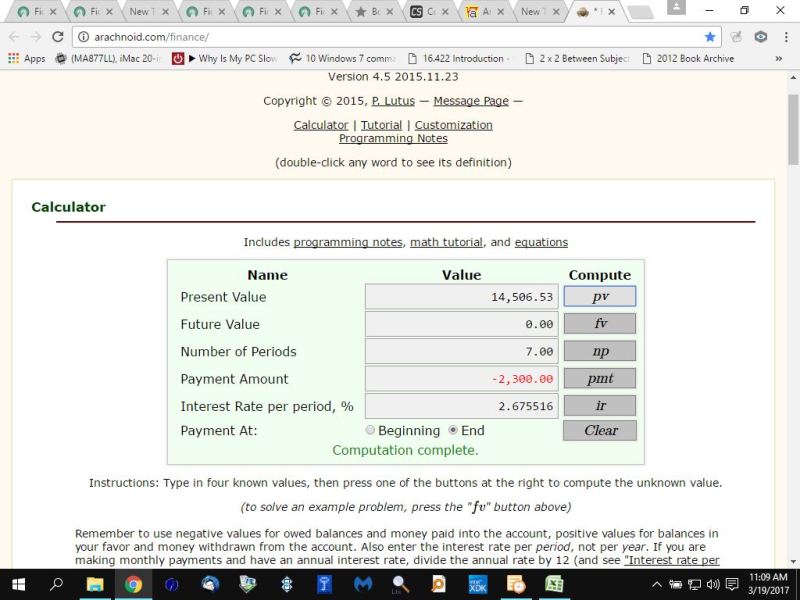
You can put this solution on YOUR website! i believe the present value will be equal to 14506.5338
your nominal annual interest rate is .04
divide that by 2 and you get a semi-annual interest rate of .02
your time periods are in semi-annual increments.
your semi-annual interest rate can be converted into an equivalent monthly rate by use of the following formula.
monthly interest rate = (1 + .01) ^ (1/6) - 1 = .00330589
the payments are made at the end of:
month 8
month 16
month 24
month 32
month 40
month 48
month 56
the present value for each of these periods would be:
2300 / 1.00330589 ^ 8 = 2240.066
2300 / 1.00330589 ^ 16 = 2181.695
2300 / 1.00330589 ^ 24 = 2124.844
2300 / 1.00330589 ^ 32 = 2069.475
2300 / 1.00330589 ^ 40 = 2015.549
2300 / 1.00330589 ^ 48 = 1963.028
2300 / 1.00330589 ^ 56 = 1911.875
add these present values up and you get 14506.53 rounded to 2 decimal places.
you should be able to use the present worth of annuity formulas also, if you translate the semi-annual interest rate into an 8 month equivalent interest rate.
that should be equal to 1.02 ^ (8/6) = 1.026755164 - 1 = .026755164
this is the equivalent 8 month effective interest rate taken from the semi-annual interest rate of 2%.
since you have 7 payments, then your present value should be equivalent to an annuity where the 8 month interest rate is .026755164 and you are taking the present value of 2300 for seven 8 month periods.
keep in mind that an interest rate of.026755164 is equal to 2.6755164%.
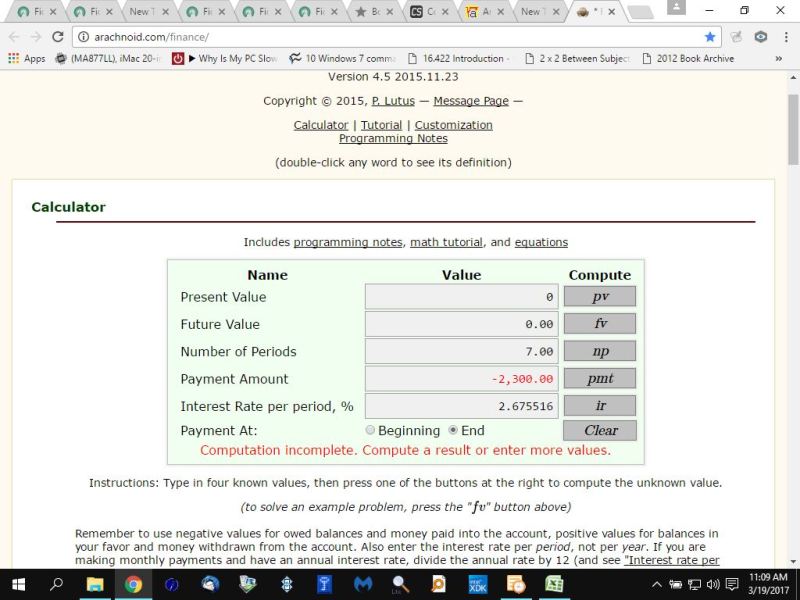
i used an online time value of money calculator to demonstrate that you will get the same present value.
using this calculator, your inputs would be as shown in the following picture.
once you click on pv, then your present value will be as shown in the following picture.
you can see that the equivalent interest rates are accurate when you look at time periods that are coincident.
for example:
8 semi-annual periods are the same as 6 eight month periods.
they are both equivalent to 48 months.
so, if you have 1000 at the end of 8 semi-annual periods, then the present value will be 1000 / 1.02 ^ 8 = 853.4903712, and if you have 1000 at the end of 6 eight month periods, then the present value will be 1000 / 1.026755164 ^ 6 = 853.4903699, and if you have 1000 at the end of 48 one month periods, then the present value will be 1000 / 1.00330589 ^ 48 = 853.4903844.
it's the same present value.
what is not considered is what happens after the 56th month.
the 5 year period is 60 months.
the assumption is that your last payment is in the 56th month and you get no more payments.
no credit is given for any payments after that, partial or otherwise.
|
|
|