|
Question 1073428: Find the cube roots of the following complex number;
-5(square root of 2)+ 5(square root of 2i)
Found 2 solutions by ikleyn, KMST:
Answer by ikleyn(52803)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I believe what you wanted was the cube roots of
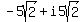 . .
You can write that as
-5sqrt(2)+i5sqrt(2) or as -5*sqrt(2)+i*5*sqrt(2) .

The three cube roots will be numbers of the form
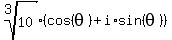 such that such that
 , ,
meaning that  for for
 . .
So,  gives us gives us
 , ,  and and  . .
You can get approximate values for 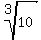
and for the trigonometric functions from a calculator.
 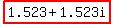
 
 
Finding exact values is a little more involved,
and the resulting expressions may not look as nice as with approximate decimals.
The one answer with  is easy, is easy,
because  , ,
so that the exact value for one of the three cube roots is
 . .
For the other two values of  , it gets a little more complicated. , it gets a little more complicated.
Since  and and  , ,
we can use the trigonometric functions for  , ,
knowing their relation to the trigonometric functions for  and and 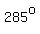 . .
For second quadrant  , ,
 and and  . .
For fourth quadrant  , ,
 and and  . .
If we want exact values, we will need to use the half-angle trigonometric formulas:
 and and  . .
 , so , so
 and and  . .
So,  and and 
That makes the exact values for the other two cube roots
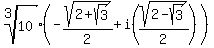 = =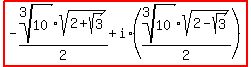 and and
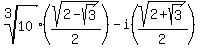 = =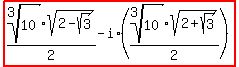 . .
|
|
|
| |