Question 1073420: Rates of Two Trains
a)Solve using on variable. Two trains depart simultaneously from a station, traveling in opposite directions. One average 80 km/h and the other 100 km/h. Determine how long it will take the trains to be 450 km apart.
b)Solve using two variables. Two trains depart simultaneously from a station, traveling in opposite directions. One average 8 km/h more than the other, and after 1/2 hour they are 100 km apart. Determine the speed of each train.
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
a) Solve using on variable. Two trains depart simultaneously from a station, traveling in opposite directions.
One average 80 km/h and the other 100 km/h. Determine how long it will take the trains to be 450 km apart.
b) Solve using two variables. Two trains depart simultaneously from a station, traveling in opposite directions.
One average 8 km/h more than the other, and after 1/2 hour they are 100 km apart. Determine the speed of each train.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
a) Let t be the time under the question.
Then the distance traveled by the first train is 80*t kilometers,
while the distance traveled by the second train is 100*t kilometers.
The equation is
80t + 100t = 450, or
180t = 450, which gives t = 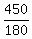 =  = 2.5 hours = 2 hours and 30 minutes.
Answer. 2.5 hours = 2 hours and 30 minutes.
b) Let x be the speed of the first train and y be the speed of the second train.
Then you have these equations:
x - y = 8, (1)
0.5x + 0.5y = 100. (2)
From (2), express x = y + 8, and substitute it into (2). You will get
0.5(y+8) + 0.5y = 100, or
0.5y + 4 + 0.5y = 100,
y = 100 - 4 ---> y = 96.
Answer. The speed of the second train is 96 km/h; of the first train 96 + 8 = 104 km/h.
Solved.
|
|
|
