Question 1073256: If p and q are the roots of the equation

Find the equation whose
roots are
 and and 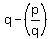
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This assignment is for those who firmly knows the Vieta's theorem and Vieta's formulas.
For the second degree polynomial (quadratic) P(x)= 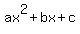 roots roots  and and  of the equation P(x)=0 satisfy of the equation P(x)=0 satisfy
 + +  = =  and and 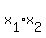 = =  . (1) (see Wikipedia, this article).
Concretely, for the given equation . (1) (see Wikipedia, this article).
Concretely, for the given equation  = 0 its roots p and q satisfy
p + q = = 0 its roots p and q satisfy
p + q =  and p*q = -2. (2)
We can state it based in Vieta's theorem even without making explicit calculations of the roots.
Now, they want we construct the quadratic equation/polynomial with the roots and p*q = -2. (2)
We can state it based in Vieta's theorem even without making explicit calculations of the roots.
Now, they want we construct the quadratic equation/polynomial with the roots 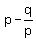 and and 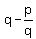 .
1. Then the coefficient at x of this polynomial, based on the Vieta's theorem, must be the opposite number to .
1. Then the coefficient at x of this polynomial, based on the Vieta's theorem, must be the opposite number to
 + + 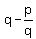 = = 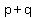 - - 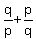 = =  - - 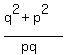 . (3)
From (2), you have . (3)
From (2), you have 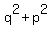 = = 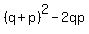 = = 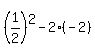 = =   = = 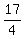 .
Therefore, we can continue and complete (3) in this way .
Therefore, we can continue and complete (3) in this way
 + + 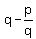 = =  - - 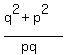 = =  = = 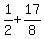 = = 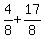 = = 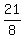 .
So, the opposite number to it, .
So, the opposite number to it, 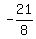 is the coefficient at x in the polynomial under the question.
2. Next step we should calculate the product is the coefficient at x in the polynomial under the question.
2. Next step we should calculate the product 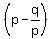 . .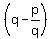 to determine the constant term of our polynomial. The product is to determine the constant term of our polynomial. The product is
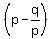 . .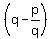 = =  - -  - -  + +  = = 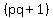 - - 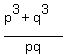 .
Now, replace pq by -2 and replace .
Now, replace pq by -2 and replace 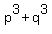 by by 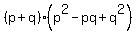 = = 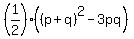 = =  = = 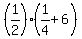 = = 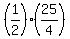 = = 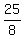 .
You will get .
You will get 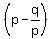 . .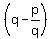 = ((-2) + 1) - = ((-2) + 1) -  = = 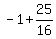 = =  .
Thus your equation under the question is .
Thus your equation under the question is 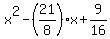 = 0.
Or, if you want to have it with integer coefficients, multiply everything by 16, and you will get = 0.
Or, if you want to have it with integer coefficients, multiply everything by 16, and you will get
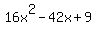 = 0. = 0.
Solved.
Using this approach, you have a priviledge of making calculations with rational numbers.
By doing it using another approach with explicit irrationalities, you will be forced to work with radicals.
It is the advantage of using Vieta's theorem.
--------------------
To extend your horizon:
The way I showed here, is THE ONLY WAY to solve the problems like this one.
The problem is especially designed and intended to teach you this method.
It is not my fantasy. It is the way you should know and the approach you must follow when solving such problems.
It may happen you will have a desire to find the roots of the original equations and then manipulate with them.
It is NOT THE WAY they want you follow in your solution.
Saying "they", I mean those who assigned you this problem.
They DEFINITELY want to know, whether you know the method I showed you, and
whether you are able to use it.
To see similar solved problems, look into the lessons
- HOW TO evaluate expressions involving  , , 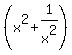 , , 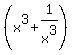 and and 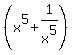
- HOW TO evaluate functions of roots of a quadratic equation
- HOW TO evaluate functions of roots of a cubic and quartic equation
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Evaluation, substitution".
Good luck and H A P P Y L E A R N I N G ! !
|
|
|