SOLUTION: Given that {{{1/(y-x)}}} , {{{1/(2y)}}} and {{{1/(y-z)}}} are consecutive terms of an arithmetric progression, prove that x, y and z are consecutive terms of a geometric progressio

Algebra ->  Sequences-and-series -> SOLUTION: Given that {{{1/(y-x)}}} , {{{1/(2y)}}} and {{{1/(y-z)}}} are consecutive terms of an arithmetric progression, prove that x, y and z are consecutive terms of a geometric progressio      Log On


   

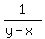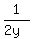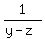Question 1073135: Given that 1%2F%28y-x%29 , 1%2F%282y%29 and 1%2F%28y-z%29 are consecutive terms of an arithmetric progression, prove that x, y and z are consecutive terms of a geometric progression
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
One nice thing about arithmetic progressions is that
if a, b, and c are three consecutive terms in an arithmetic progression (AP),
a + c = 2b (and if a + c =2b, a, b, and c form an AP).
That means that
1%2F%28y-x%29%2B1%2F%28y-z%29=2%281%2F2y%29
%28%28y-z%29%2B%28y-x%29%29%2F%28%28y-x%29%28y-z%29%29=1%2Fy
%282y-x-z%29%2F%28y%5E2-xy-zy%2Bxz%29=1%2Fy
y%282y-x-z%29=y%5E2-xy-zy%2Bxz
2y%5E2-xy-zy=y%5E2-xy-zy%2Bxz
Cancelling like terms,
2y%5E2=y%5E2%2Bxz
highlight%28y%5E2=xz%29

One nice thing about geometric progressions is that
if x, y, and z are three consecutive terms in a geometric progression (GP),
xz=y%5E2 , and if xz=y%5E2 then x, y, and z form a GP,
and that is exactly what we found above.