|
Question 1073098: A farm co-op has 6000 acres available to plant with corn and soybeans. Each acre of corn requires 9 gallons of fertilizer/herbicide and 3/4 hour of labor to harvest. Each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1 hour of labor to harvest. The co-op has available at most 40,500 gallons of fertilizer/herbicide and at most 5250 hours of labor for harvesting. The number of acres of each crop is limited (constrained) by the available resources: land, fertilizer/herbicide, and labor for harvesting. Let x represent the number of acres of corn and y represent the number of acres of soybeans.
Write the system of inequalities that describes the farm's constraints.
What is the most number of acres of corn and soybeans that the farm could plant, treat with fertilizer/herbicide and harvest?(TIP: solve the system of inequalities and identify the extreme point(s) of the region of solution).
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52810)   (Show Source):
You can put this solution on YOUR website! .
A farm co-op has 6000 acres available to plant with corn and soybeans.
Each acre of corn requires 9 gallons of fertilizer/herbicide and 3/4 hour of labor to harvest.
Each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1 hour of labor to harvest.
The co-op has available at most 40,500 gallons of fertilizer/herbicide and at most 5250 hours of labor for harvesting.
The number of acres of each crop is limited (constrained) by the available resources: land, fertilizer/herbicide,
and labor for harvesting. Let X represent the number of acres of corn and Y represent the number of acres of soybeans.
Write the system of inequalities that describes the farm's constraints.
What is the most number of acres of corn and soybeans that the farm could plant, treat with fertilizer/herbicide and harvest?
(TIP: solve the system of inequalities and identify the extreme point(s) of the region of solution).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The system of inequalities:
x >= 0
Y >= 0
X + Y <= 6000 (the area constraint)
9X + 3Y <= 40500 (the fertilizer/herbicid constraint)
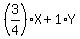 <= 5250 (labor hours constraint).
The next assignment was formulated INACCURATELY, so I will not move further.
Actually, after reaching this point, all you need to do is to find free of charge solver in the Internet for linear programming tasks,
then input these inequalities and press the "SOLVE" button.
Also, look into the lesson
- Solving minimax problems by the Linear Programming method
to see the examples of solved problems on the linear programming method and to learn the methodology.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! x = number of acres of corn
y = number of acres of soybeans
you are given that the total number of acres can't be greater than 6000.
the inequality for this is:
x + y <= 6000
each acre of corn requires 9 gallons of fertilizer/herbicide and 3/4 hours of labor.
each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1 hour of labor.
you are given that the number of gallons of fertilizer/herbicide can't exceed 40,500.
since each acre of corn requires 9 gallons of fertilizer/herbicide and each acre of soybeans requires 3 gallons of fertilizer/herbicide, you get:
9x + 3y <= 40500
you are given that the number of hour of labor can't exceed 5250.
since each acre of corn requires 3/4 hour of labor and each acre of soybeans requires 1 hour of labor, you get:
3/4 * x + y <= 5250
since the number of acres can't be less than 0, 2 other constraints are:
x >= 0
y >= 0
your total constraints are:
x + y <= 6000
9 * x + 3 * y <= 40500
3/4 * x + y <= 5250
x >= 0
y >= 0
using the desmos.com calculator, you easiest way to see the region of feasibility is to graph the opposite of these inequalities.
in other words, you would graph:
x + y >= 6000
9 * x + 3 * y >= 40500
3/4 * x + y >= 5250
x <= 0
y <= 0
the area of the graph that is not shaded will be your region of feasibility.
the graph looks like this:
the corner points of the feasible region are:
(0,5250)
(3000,3000)
(3750,2250)
(4500,0)
your maximum acres will be at those corner points.
it appears that your maximum acres are 6000 and this occurs at (3000,3000) and at (3750,2250)
all the constraints have to be satisfied.
at (3000,3000), you will be utilizing 3000 * 9 + 3000 * 2 = 36000 gallons of fertilizer/herbicide and you will be utilizing 3000 * 3/4 + 3000 * 1 = 5250 hours of labor.
at (3750,2250), you will be utilizing 3750 * 9 + 2250 * 3 = 40500 gallons of fertilizer/herbicide and you will be utilizing 3750 * 3/4 + 2250 * 1 = 5062.5 hours of labor.
all the constraints are met at both these corner points and you can plow the same acreage at both of these corner points, so you have two possible corner points that give you the same maximum number of acres solution.
since you are asked for the maximum number of acres that can be planted, the answer is 6000.
the desmos.com calculator can be found at:
https://www.desmos.com/calculator
|
|
|
| |
