Question 1072760: Tracy and Kelly are running laps on the indoor track — at steady speeds, but in opposite directions. They meet every 20 seconds. It takes Tracy 45 seconds to complete each lap. How many seconds does it take for each of Kelly’s laps? (Answer must be checked as well)
Found 2 solutions by ikleyn, josmiceli:
Answer by ikleyn(52817)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When Tracy and Kelly are running on the track in opposite directions, the distance they cover together from one meeting point
to the next meeting point is exactly the length of the track D.
It is the key moment to understand solving this problem.
Therefore, if "t" and "k" are the rates of each girl/women, then their summary (combined) rate is
t + k =  per second in terms of the length D, (1)
where D is the length of the track.
From the other side, we know that the Tracy's rate is t = per second in terms of the length D, (1)
where D is the length of the track.
From the other side, we know that the Tracy's rate is t = 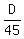 per second in terms of the length D.
Therefore, from (1) we have
k = per second in terms of the length D.
Therefore, from (1) we have
k = 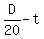 = = 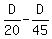 = = 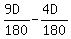 = = 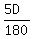 = = 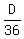 .
Thus, Kelly's rate is k = .
Thus, Kelly's rate is k = 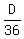 per second in terms of D.
It means that Kelly will cover the entire distance D (one lap) in per second in terms of D.
It means that Kelly will cover the entire distance D (one lap) in 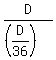 = 36 seconds.
Answer. Kelly's lap will take 36 seconds.
In other words, Kelly's rate is = 36 seconds.
Answer. Kelly's lap will take 36 seconds.
In other words, Kelly's rate is 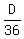 , while Tracy's rate is , while Tracy's rate is 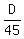 .
Check. Their combined rate when they are running in opposite directions is .
Check. Their combined rate when they are running in opposite directions is
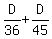 = =  = = 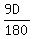 = =  . Check ! . Check !
This Travel and Distance problem is close (by the method of solution) to Joint-work problems.
On relevant Joint-work problems see the lessons
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Selected joint-work word problems from the archive
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
In this textbook, you will find "Travel and Distance" problems, as well as "joint work" problems.
H a p p y l e a r n i n g ! !
Answer by josmiceli(19441)   (Show Source): (Show Source):
|
|
|