Question 1072712: how do you use the intermediate value theorem to prove that f(x)= x^3 -9x +5 has a real zero in each of the following intervals: [-4, -3], [0,1], and [2, 3]
Found 2 solutions by Fombitz, ikleyn:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Check the value at the endpoints.
If one is positive and one is negative then the functions crosses zero in between the two points.
I'll do one interval, you do the other two.
[0,1]


So there must be a zero in [0,1].
Do the same for the other two intervals.
Answer by ikleyn(52898)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From Wikipedia, this article:
In mathematical analysis, the intermediate value theorem states that if a continuous function, f, with an interval, [a, b],
as its domain, takes values f(a) and f(b) at each end of the interval, then it also takes any value between f(a) and f(b)
at some point within the interval.
This has two important corollary: If a continuous function has values of opposite sign inside an interval, then
it has a root in that interval (Bolzano's theorem).
f(x)= x^3 -9x +5 has a real zero in each of the following intervals: [-4, -3].
f(x) at the ends of the given interval:
f(-4) =  = -23;
f(-3) = = -23;
f(-3) = 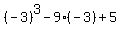 = 5.
Now compare the signs of (f-4) and f(-3) and apply the theorem. = 5.
Now compare the signs of (f-4) and f(-3) and apply the theorem.
For other cases, try the same.
|
|
|