Question 1072666: Peter is standing on a bridge and throws a stone up into the air at 30 m/s. The stone hits the surface of the water below 10 seconds later. From what height above the surface of the water did Peter throw the stone? (Note: the acceleration due to gravity is 10 m/s^2 )
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! WITHOUT FORMULAS:
The initial upwards speed was 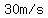 . .
For 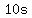 , that upwards speed decreased linearly due to gravity , that upwards speed decreased linearly due to gravity
by 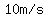 each each  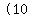   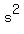  , ,
for a total decrease of 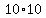  
to  . .
The average upwards speed for those 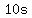 was was
   . .
At an average speed of   for for 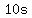 , ,
the stone's upwards displacement was
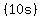 
So, the stone left Peter's hand  above the surface of the water. above the surface of the water.
WITH FORMULAS:
You may have learned in physics class that, for an object moving linearly under constant acceleration,
its position 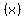 as a function of time as a function of time 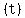 can be modeled as can be modeled as
 , where , where
 is the constant acceleration, while is the constant acceleration, while
 and and  are respectively the position and velocity of the object at are respectively the position and velocity of the object at  . .
You could choose to measure position as height (in meters) above the water surface,
and time (in seconds) since the stone left Peter's hand.
In that case, distance above the water, upwards velocity and upwards acceleration are positive,
so initial velocity is  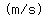 , ,
acceleration is  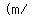 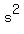  , ,
 is what you are looking for , is what you are looking for ,
and you know that  at at  . .
Substituting into 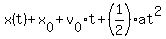 , ,
 , ,
 , ,
 , and , and  (in meters , of course). (in meters , of course).
|
|
|