Question 1072417: find the domain and range of f(x)=3x^2+2X-4
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The domain is all real numbers,
as it is for all polynomials.
For polynomials of odd degree, the range is all real numbers.
The function in this problem is a quadratic polynomial
(a polynomial of degree 2).
Polynomials of degree 2 can be written in the form
 with real number coefficients with real number coefficients
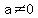 , ,  , and , and  . .
If  the quadratic polynomial has a maximum. the quadratic polynomial has a maximum.
If  (as for (as for  in this case), in this case),
the polynomial has a minimum at  . .
So, this polynomial, with  , ,
has a minimum at  , ,
and that minimum is

For all real values of  , ,  . .
As 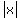 increases, so does increases, so does  , without bound, , without bound,
taking all possible real  values. values.
That is the range.
|
|
|