SOLUTION: how many distinct permutations can be formed from all the letters of the word SUCCESS

The word SUCCESS is a 7-letter word.  The answer would be 7! 
for a 7-letter word like PAINTER, for you can tell all those 
letters apart.  But in SUCCESS, the 3 S's cannot be told apart,
nor can the 2 C's.  So we must divide 7! by the number of ways 
the 3 S's could be arranged in each permutation, which is 3!, 
as well as divided by the number of ways the two C's could be 
arranged, which is 2!.

Answer: 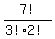  = 420 ways

Edwin