Question 1072350: Solve sin 4x = cos 2x
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! sin 4x=2 sin 2x*cos 2x
That equals cos 2x
divide by cos 2x
2 sin 2x=1
sin 2x=(1/2)
x=pi/12
----------
check
sin pi/3 should equal cos pi/6
This is true.
Answer by ikleyn(52834)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
sin(4x) = cos(2x) ---> 2sin(2x)*cos(2x) = cos(2x) ---> 2sin(2x)*cos(2x) - cos(2x) = 0 --->
cos(2x)*(2sin(2x)-1) = 0.
The last equation deploys in two independent equations:
1. cos(2x) = 0 ----> x =  , x = , x =  , x = , x =  and x = and x =  2. 2sin(2x)-1 = 0 ----> sin(2x) =
2. 2sin(2x)-1 = 0 ----> sin(2x) =  , which implies
2x = , which implies
2x =  and/or 2x = and/or 2x = 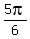 .
This, in turn, implies that the original equation has 4 (four) solutions in the interval 0 <= x < .
This, in turn, implies that the original equation has 4 (four) solutions in the interval 0 <= x <  :
x = :
x = 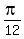 , x = , x = 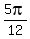 , x = , x = 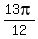 and x = and x = 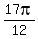 .
Answer. In all, there are 8 solutions: x = .
Answer. In all, there are 8 solutions: x =  , x = , x =  , x = , x =  , x = , x =  ; x = ; x = 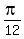 , x = , x = 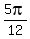 , x = , x = 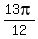 , x = , x = 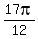 . .
Solved.

Plots y = sin(4x) (red) and y = cos(2x) (green)
To see more examples of solved trigonometry equations with detailed solutions, look into the lessons
- Solving simple problems on trigonometric equations
- Solving typical problems on trigonometric equations
- Solving more complicated problems on trigonometric equations
- Solving advanced problems on trigonometric equations
- OVERVIEW of lessons on calculating trig functions and solving trig equations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Trigonometry: Solved problems".
The solution by "Boreal" is wrong, since it does not cover a lot of roots.
|
|
|