SOLUTION: Find the equation of the ellipse with the following properties. Express your answer in standard form. Vertices at ( 1, 5 ) and ( 7, 5 ) e = 1/3

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Find the equation of the ellipse with the following properties. Express your answer in standard form. Vertices at ( 1, 5 ) and ( 7, 5 ) e = 1/3       Log On


   

Question 1072280: Find the equation of the ellipse with the following properties. Express your answer in standard form.
Vertices at ( 1, 5 ) and ( 7, 5 ) e = 1/3
Answer by ikleyn(52877) About Me  (Show Source):
You can put this solution on YOUR website!
.
Since the condition says "Vertices are at (1,5) and (7,5)", it means


     a)  the vertices lie on the horizontal line  y = 5,   and


     b)  the major axis length is 7 - 1 = 6. Thus the major semi-axis is  a = 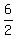6%2F2 = 3.


Since eccentricity is e = 1%2F3, the linear eccentricity is c = a*e = 1, which means that

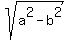sqrt%28a%5E2-b%5E2%29 = 1  ====>  9%5E2+-+b%5E2 = 1%5E2  ====>  b%5E2 = 9-1 = 8,

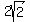where b = sqrt%288%29 = 2sqrt%282%29 is the minor semi-axis.


Thus the equation of the ellipse is 

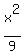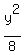x%5E2%2F9 + y%5E2%2F8 = 1.


For the related terminology see the lesson

    - Ellipse definition, canonical equation, characteristic points and elements  

in this site.