Question 1071888: Convert to trigonometric form:  square root of 3 space plus space 4 i square root of 3 space plus space 4 i
A.) 8(cos60 + i sin60)
B.) 8(cos30 + i sin30)
C.) 8(sin30 + i cos30)
D.) 8(sin60 + i cos60)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
 and and  , so , so

TIP:
If they give you a complex number with
a non-zero real part, and
a different non-zero imaginary part,
and the angle has to be a nice round number,
one part will be  or or 
times the other part,
Because the only exact angles with
non-zero, different, and simple-to-write
cosine and sine are  , ,  in quadrant 1, in quadrant 1,
and angles symmetrical to those in the other quadrants.
 and and
 . .
If both parts are positive, it is one of those angles.
If there are negative parts,
it is a symmetrical angle on another quadrant.
For example, 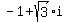
has a negative real part, and a positive imaginary part,
so it would be plotted in quadrant 2.
The real part has to be cosine times something,
so it is 
The quadrant 1 angle with  for a cosine for a cosine
is  . .
To get the symmetrical angle from quadrant 2,
You subtract from  , ,
to get  in quadrant 2. in quadrant 2.
So,
 . .
If both parts are negative,
the complex number would be plotted in quadrant 3,
where the angle would be  plus plus
the symmetrical reference angle from quadrant 1.
If the real part is positive,
and the imaginary part negative,
You are in quadrant 4,
and the angle is  minus minus
the quadrant 1 angle.
FORMULAS:
Any complex number,
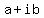 , ,
with  , and , and  being real numbers, being real numbers,
can always be written as
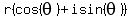
The formulas for  and and  are: are:


and
 . .
The last 2 formulas allow you to find theta
(in degrees or radians) with any scientific calculator.
If the calculator gives you a negative angle, add  (or (or  when working in radians). when working in radians).
(For faster calculations, you can use
 and the signs, positive or negative, of and the signs, positive or negative, of  and and  ). ).
|
|
|