Question 1071655: (1.)Find the number of terms in an A. P whose sum is 1340 with the first term being 3 and the nth term 131.
(2.) The 8th term of an A. P is 9 greater than the 5th term, and the 10th is 10 times the 2nd term. Find the 6th term.
(3.) How many terms of the sequence 3+5+7+........are needed for the sum to equal 288?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! SHOW YOUR WORK WAY:
This often requires writing formulas as your teacher wrote in class,
and then substituting the numbers given.
The way your teacher wrote the formulas could be a little different from the way I (or other tutors in this site) do it.
My AP definitions:
 = the first term of an AP
 = term number  of an AP
 = the common difference of an AP
 = the sum of the first terms of an AP
My AP formulas:
I never memorized the formula below, that derives from the two above
USING WORDS AND IDEAS TO UNDERSTAND AND REASON TO THE PROBLEM:
Trying to explain how to get to the answer may get wordy.
A teacher may have a favorite way to get to the answer, and reject all other ways.
However, it is useful to know more than one way
and at times you need to use the fastest way to the answer
(1) In words (and important ideas):
The sum of consecutive terms of an AP is
the number of terms added (n) times
the average of the first and last terms added.
We have the first and last terms, and we need the number of terms,
so the formula (in words) above is the one we need to use.
The average of first and last terms added is 
Dividing, we find  .
(The average of the first and last terms added is
 in formulas,
and that explains 
as one way to write the formula for the sum).
Using the formulas, you write
 --->  .
(2) Using the formulas, you write
,
and then you could write and simplify
the expressions for 8th, 5th, 10th and 2nd terms,
before you start using those expressions
to make equations withe the clues given in the problem:
 ,
 ,
 , and
 .
The clues are  , and  ,
so we have
 , and 
as two equations forming a system of two linear equations
to find variables and from.
Luckily it is an easy system
 --> --> --> --> -->
Now we can use the values found for and ,
along with formula ,
to find the 6th term asked for
 --> 
(2) In words (and important ideas):
You know that AP is what we call a sequence of numbers we call "terms"
where we get from one "term" to the next by adding a certain number.
(We always add the same number ,
and we call that number the common difference).
To go from the 5th to the 8th term, we need to add
 times.
Since the total added was  ,
to find we divide
 .
We do not know any of the terms,
but we know that to get from the 2nd term to the 10th term
we have to add  times  .
So, the difference between those two terms is  ,
but that must be  times the second term,
because "the 10th is 10 times the 2nd term."
So, the 2nd term is  .
To get from that 2nd term to the 6th term,
we have to add  times  .
So,  
(3) In words (and important ideas):
That is the sum of an AP where each term is the one before plus 2.
All the terms are odd numbers, but the sum is an even number.
You know that there must be an even (n) number of terms,
because if you add an odd number of odd numbers, the sum is odd.
I know that the sum of consecutive terms of an AP is
the number of terms added (n) times
the average of the first and last terms added.
Could it be  ?
Since it is an AP,
the 10th term is  more than first term  .
The 10th term is 
The sum of the first  terms would be
the average of first and 10th term is 
Then, the sum of the first  terms is  .
The next terms will start with  ,
end with 20th term  ,
so they will add to a lot more than  ,
and the sum to  will add to more than  .
Could it be  ?
For ,   ,
and the sum to is
 .
So  terms are needed for the sum to equal 288.
(3) Using the formulas, you write
,
You use the clues
 and  to substitute into ,
and get  --> --> .
Then substituting the values for , , and  into , you get
That is an easy quadratic equation.
You can rewrite it as 
and find the solutions by factoring (it works in this case),
or by using the quadratic formula (it works in all cases).
You know because of the minus sign in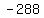 
that one of the solutions to the equation will be negative,
so the solution to the problem is the other, positive solution to the equation.
You can also "complete the square":
 --->  --> 
because we know  is positive.
|
|
|
