 The green line above, drawn between foci, is given to
be 10 units long. The center is its midpoint, so the
two foci are (4,4) and (4,-6).
The two blue lines are the latus rectums. They are given
as 9/2, so by subtraction of half that or 9/4 from
the x-coordinate of the focus (4,4), we get that
the left end of the upper latus rectum is the point
(7/4,4). The hyperbola goes through that point.
We know that the equation of the hyperbola is of the
form
The green line above, drawn between foci, is given to
be 10 units long. The center is its midpoint, so the
two foci are (4,4) and (4,-6).
The two blue lines are the latus rectums. They are given
as 9/2, so by subtraction of half that or 9/4 from
the x-coordinate of the focus (4,4), we get that
the left end of the upper latus rectum is the point
(7/4,4). The hyperbola goes through that point.
We know that the equation of the hyperbola is of the
form
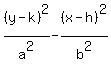

 and since the center is (4,-1), it's
and since the center is (4,-1), it's
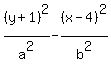

 or
or
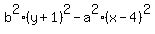

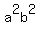 Since it goes through (7/4,4), we substitute that
for (x,y)
Since it goes through (7/4,4), we substitute that
for (x,y)
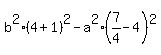

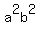
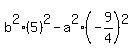

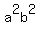
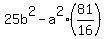

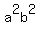
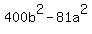

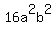 We know that c = 5 because c is the distance from the
center to the focus.
For all hyperbolas,
We know that c = 5 because c is the distance from the
center to the focus.
For all hyperbolas, 

 or
or 

 ,
and so
,
and so 

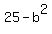 Substitute in
Substitute in
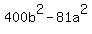

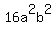
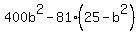

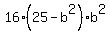
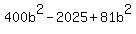

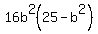
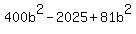

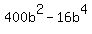
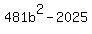

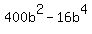
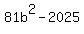

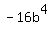
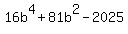


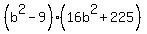


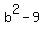

 ;
; 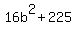




 ;
; 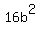




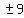 ;
; 

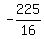 bē can only be positive, so
bē = 9
Substitute in
bē can only be positive, so
bē = 9
Substitute in


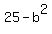


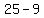


 So the equation:
So the equation:
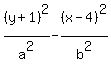

 becomes:
becomes:
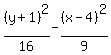

 Edwin
Edwin