SOLUTION: I need assistance in finding the sin(x/2), cos(x/2), and tan(x/2) from: {{{sec(x) = 4/3}}} with 270 degrees < x < 360 degrees sin(x/2) = cos (x/2) = tan (x/2) = Step by st

Algebra ->  Trigonometry-basics -> SOLUTION: I need assistance in finding the sin(x/2), cos(x/2), and tan(x/2) from: {{{sec(x) = 4/3}}} with 270 degrees < x < 360 degrees sin(x/2) = cos (x/2) = tan (x/2) = Step by st      Log On


   

Question 1071585: I need assistance in finding the sin(x/2), cos(x/2), and tan(x/2) from: sec%28x%29+=+4%2F3 with 270 degrees < x < 360 degrees
sin(x/2) =
cos (x/2) =
tan (x/2) =
Step by step solutions is most appreciated. Thank you.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Look at "Half angle formulas" on Wikipedia.

Answer by ikleyn(52884) About Me  (Show Source):
You can put this solution on YOUR website!
.
I need assistance in finding the sin(x/2), cos(x/2), and tan(x/2) from: sec%28x%29+=+4%2F3 with 270 degrees < x < 360 degrees
sin(x/2) =
cos (x/2) =
tan (x/2) =
Step by step solutions is most appreciated. Thank you.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

0.  Since sec(x) = 4%2F3, it implies that cos(x) = 3%2F4.


1.  Now, according to the formulas for the half argument,

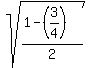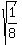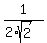    sin(x/2) = %2Bsqrt%28%281-cos%28x%29%29%2F2%29 = %2Bsqrt%28%281-%283%2F4%29%29%2F2%29 = %2Bsqrt%28%281%2F4%29%2F2%29 = sqrt%281%2F8%29 = 1%2F%282%2Asqrt%282%29%29 = sqrt%282%29%2F4. 

    Notice that the sign at sqrt is "+" (plus), because the angle x%2F2 lies in QII, where sine is positive. 



2.  Next, according to the formulas for the half argument,

    cos(x/2) = -sqrt%28%281%2Bcos%28x%29%29%2F2%29 = -sqrt%28%281%2B%283%2F4%29%29%2F2%29 = -sqrt%28%287%2F4%29%2F2%29%29 = -sqrt%287%2F4%29 = -sqrt%287%29%2F2.

    Notice that the sign at sqrt is "-" (minus), because the angle x%2F2 lies in QII, where cosine is negative. 


3.  Just having  sin(x/2) = sqrt%282%29%2F4  and  cos(x/2) = -sqrt%287%29%2F2,  you can calculate tan(x/2)  as their ratio:

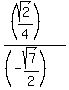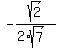    tan(x/2) = %28%28sqrt%282%29%2F4%29%29%2F%28%28-sqrt%287%29%2F2%29%29 = -sqrt%282%29%2F%282%2Asqrt%287%29%29 = -sqrt%2814%29%2F14%29

Regarding formulas for trigonometric functions of half argument,  see the lesson
    - FORMULAS FOR TRIGONOMETRIC FUNCTIONS
    - Trigonometric functions of half argument
in this site.

Also,  you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic "Trigonometry. Formulas for trigonometric functions".

Also see the topic "Trigonometry: Solved problems" of this textbook.