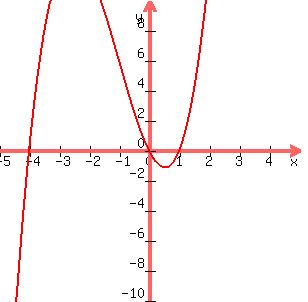
Question 107150: the problems is to write the equation of a polynomial function with the given characteristics. Use a leading coefficient of 1 or -1 and make the degree as small as possible. Crosses the x- axis at -4, 0 and 1; lies above the x axis between -4 and 0; lies below the x - axis between o and 1. I have searched the internet and my textbook but can not find how to solve this problem. the question is one that my teacher gave us it is not in the textbook.
Found 2 solutions by Fombitz, stanbon:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Crosses the x axis at -4,0,1, in other words f(x)=0.
It must have a form like at least like this,
f(x)=g(x)*(x+4)*x*(x-1)
because
at x=-4, x+4=0, f(x)=0
at x=0, x=0, f(x)=0
at x=1, x-1=0, f(x)=0
We'll get to g(x) later.
OK, now we satisfy the crossing conditions.
Let's look at what happens between (-4,0) and (0,1).
Between (-4,0), x+4>0, x<0, and x-1<0.
If you multiply the product of those you would have positive times negative times negative which would give me positive, that is, lies above the x axis. The function g(x) would have to be positive in this range also.
Between (0,1), x+4>0, x>0, and x-1<0.
If you multiply the product of those you would have positive times positive times negative which would give me negative, that is, lies above the x axis. The function g(x) would have to be positive in this range also.
Since you satisfy the conditions for above and below the x axis in the given ranges and you cross the x axis at the right points, we're almost done.
Now for g(x). You can make it as complicated as I want as long as it stays positive in the given ranges(Example:g(x)=x*x).
You also want to make the degree of the polynomial as small as possible.
So let's make g(x) as simple as can be.
Let's make g(x)=1.
Therefore,

satisfies all of your criteria.
If you want to expand it, it would be,

Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! the problems is to write the equation of a polynomial function with the given characteristics. Use a leading coefficient of 1 or -1 and make the degree as small as possible. Crosses the x- axis at -4, 0 and 1; lies above the x axis between -4 and 0; lies below the x - axis between o and 1.
----------
1st: f(x) = x(x+4)(x-1) or
2nd: f(x) = -x(x+4)(x-1)
Check to see which one has f(-2) > 0 , that is " above the x-axis".
------------------
1st equation:
f(-2)= -2(2)(-3)= 12 > 0
-----------
2nd equation:
f(-2) =-[-2(2)(-3)] = -12 < 0
--------------
1st equation is the one you want
--------------
Cheers,
Stan H.
|
|
|