|
Question 1071489: A system containing a circle and a parbola has 3 solutions. Find the system ( set of equations of the circle and the parbola) using the following information. Show your work.
・The center of the circle is at the origin (0,0)
・The parbola opens upward.
・The vertex of parbola is on the y=axis.
・one of the solutions is (root(7),3).
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A circle with radius 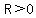 and center at the origin (0,0) and center at the origin (0,0)
has the equation
 . .
A parabola, opening upwards, and with its vertex on the y-axis
has the equation
 , with some constants , with some constants  , and , and  . .
Such a parabola has the y-axis as its axis of symmetry.
You could also say the the y-axis is an axis of symmetry for
the circle with radius  and center at the origin (0,0). and center at the origin (0,0).
As a consequence of this y-axis symmetry, for every solution of this system
(intersection point of the parabola and circle),
its reflection across the y-axis will also be a solution.
The only way to get 3 solution is for the odd solution to be
its own reflection across the y-axis image,
meaning that the odd intersection point is on the y-axis.
The circle crosses the y-axis at points (0,R) and (0,-R).
One of those points must be a point of the parabola,
specifically the point with  , ,
parabola vertex 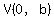 . .
So, it is either 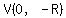 , or , or 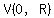 , ,
but a parabola opening upwards with vertex 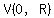
would have 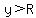 for all points other than the vertex, for all points other than the vertex,
and would touch the circle only at that one point,
meaning that the system would have only one solution.
So,  , , 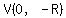 is the vertex, is the vertex,
and  is the equation of the parabola. is the equation of the parabola.
The point 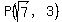 is a solution, so it is is a solution, so it is
a point of the circle and a point of the parabola.
Substituting into  , we get , we get



The equation for the circle is  , ,
and  --> -->  --> --> 
Substituting that value,
and the coordinates of 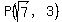 into into  , we get , we get



 --> -->  --> -->  , ,
and the equation for the parabola is

So, the system the problem asks us to "reverse-engineer" for is
 . .
|
|
|
| |