SOLUTION: Find the range of k in the of equations below if this system has 2 real solutions. Show your work. y=(x-1)^2+3 & y=2x+k

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Find the range of k in the of equations below if this system has 2 real solutions. Show your work. y=(x-1)^2+3 & y=2x+k      Log On


   

Question 1071488: Find the range of k in the of equations below if this system has 2 real solutions. Show your work. y=(x-1)^2+3 & y=2x+k
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
system%28y=2x%2Bk%2Cy=%28x-1%29%5E2%2B3%29 --> system%28k=y-2x%2C%28x-1%29%5E2%2B3%29=2x%2Bk%29 --> system%28k=y-2x%2Cx%5E2-2x%2B1%2B3=2x%2Bk%29 --> system%28k=y-2x%2Cx%5E2-2x%2B4-2x-k=0%29 --> system%28k=y-2x%2Cx%5E2-4x%2B4-k=0%29
If we chose a real k so that x%5E2-4x%2B4-k=0 has 2 real solutions for x ,
we will have the corresponding real solutions for y=2x%2Bk .
For a quadratic equation ax%5E2%2Bbx%2Bc=0 to have 2 real solutions
(which could both be the same)
it must be b%5E2-4ac%3E=0 .
For the two real solutions to be different we need b%5E2-4ac%3E0 .
So, in the case of x%5E2-4x%2B4-k=0 ,
where a=1, b=-4 and c=4-k ,
to have 2 real solutions (which could both be the same) we must have
%28-4%29%5E2-4%2A1%2A%284-k%29%3E=0 --> 16-4%284-k%29%3E=0 --> 16-16%2B4k%3E=0 --> 4k%3E=0 --> highlight%28k%3E=0%29 .
As an interval it would be %22%5B+0+%2C%22infinity%22%29%22 .

If we wanted to have two different real solutions,
we would need to have 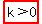highlight%28k%3E0%29 ,
and in interval notation that would be 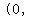%22%28+0+%2C%22infinity%22%29%22 .

IF YOU WERE STUDYING CALCULUS,
the answer would be obvious, if somewhat hard to explain the reasoning.
You would know that the slope of the tangent to y=%28x-1%29%5E2%2B3%29
is dy%2Fdx=2%28x-1%29 ,
and since the slope of y=2x%2Bk is 2 ,
the slope of both functions would be the same when
2%28x-1%29=2 <--> x-1=1 <--> x=2 .
That point could be the point of tangency if
both functions have the same y value for x=2 .
That would happen for a real k such that at x=2 <--> x-1=1
%28x-1%29%5E2%2B3=2x%2Bk , meaning that
1%5E2%2B3=2%2A2%2Bk
4=4%2Bk <---> k=0 .
That point of tangency would be (2,4), with y=2%2A2%2B0=4 .
For x=2 <--> x-1=1 ,
the function y=%28x-1%29%5E2%2B3%29 has y%282%29=4 at x=2 .
For k=0 both functions would have the y%282%29=4 at x=2 graph%28300%2C300%2C-1%2C4%2C-2%2C8%2C-3%2C-4%2C%28x-1%29%5E2%2B3%2C2x%29
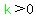If green%28k%29%3E0 function y=2x%2Bgreen%28k%29 will have y%282%29=2%2A2%2Bgreen%28k%29=4%2Bgreen%28k%29%3E4 , and will be passing through a point inside the parabola, crossing it twice:
If 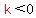red%28k%29%3C0 function y=2x%2Bred%28k%29 will have y%282%29=2%2A2%2Bred%28k%29=4%2Bred%28k%29%3C4 , and will be below the point (2,4) where the slope of y=%28x-1%29%5E2%2B3%29 is 2 ,
and since the slope of y=%28x-1%29%5E2%2B3%29 increase with increasing x,
the function y=2x%2Bred%28k%29 , with its constant slope=2 will never be able to catch up.
graph%28300%2C300%2C-1%2C4%2C-2%2C8%2C2x-1.2+%2C2x%2B0.8%2C%28x-1%29%5E2%2B3%2C2x%29