SOLUTION: Two cars start from towns 420 miles apart and travel toward each other. They meet at 4 HR. Find the speed of each car if one travels 15 mph faster than the other.

Algebra ->  Finance -> SOLUTION: Two cars start from towns 420 miles apart and travel toward each other. They meet at 4 HR. Find the speed of each car if one travels 15 mph faster than the other.      Log On


   

Question 1071439: Two cars start from towns 420 miles apart and travel toward each other. They meet at 4 HR. Find the speed of each car if one travels 15 mph faster than the other.
Answer by ikleyn(52775) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let r be the speed of the faster car, in mph.
Then the speed of the slower one is (r-15) mph.

The "distance" equation is

4*r + 4*(r-15) = 420.

4r + 4r - 60 = 420,

8r = 420 + 60,

8r = 480  --->  r = 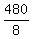480%2F8 = 60.


Answer.  The speed of the faster car is 60 mph. That of the slower car is 60-15 = 45 mph.

Solved.