Question 1071217: in 2000, a company had 1132 stores nationwide. by 2002, this total had grown to 1525. if the number of stories continues to grow exponentially at the same rate, how many stores will there be in 2016?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39630)   (Show Source):
You can put this solution on YOUR website! If you take time for year 2000 as 0 time and identify your cartesian points as (0,1132) and (2,1525), but need a specified growth model which is EXPONENTIAL, try starting with  . Not a linear formula; but it is exponential.
Which corresponds to a linear equation form y=mx+b.
Note:  .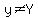
The points you want now, are (0, ln(1132) ) and (2, ln(1525) ).
Do you know how to use THESE two points to find an equation for a line in SLOPE-INTERCEPT form, and identify the vertical axis intercept and the slope? If you do and can, do you know how to use the equation to find how many stores in the year 2016?
You should find and translate back to  .
Let x=16, for year 2016 and find Y.
Answer by MathTherapy(10557)  (Show Source):
You can put this solution on YOUR website! in 2000, a company had 1132 stores nationwide. by 2002, this total had grown to 1525. if the number of stories continues to grow exponentially at the same rate, how many stores will there be in 2016?
With x being number of years since year 2000, and y, the number of stores, we get the following points: (0, 1,132) and (2, 1,525)
Point (0, 1,132)
Exponential function: 
 --------- Substituting (0, 1,132) for (x, y)
1,132 = a -------- eq (i)
---------------------------------------------
Point (2, 1,525)
Exponential function: 
 --------- Substituting (2, 1,525) for (x, y), and 1,132 for a
---------------------------------------------
Exponential function: 
With x being 16 (year 2016), y, or number of stores in 2016 = 
|
|
|
