Question 1070600: The speed of the current in a river is 6 mph. A ferry operator who works that part of the river is looking to buy a new boat. Every day, his route takes him 22.5 miles against the current and back to his dock, and he needs to make this trip in a total of 9 hours. he has a boat in mind, but he can only test in on a... show more he speed of the current in a river is 6 mph. A ferry operator who works that part of the river is looking to buy a new boat. Every day, his route takes him 22.5 miles against the current and back to his dock, and he needs to make this trip in a total of 9 hours. he has a boat in mind, but he can only test in on a lake where there is no current. How fast must the boat go on the lake in order for it to serve the ferry operator's needs?
Answer by ikleyn(52867)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The speed of the current in a river is 6 mph. A ferry operator who works that part of the river is looking to buy a new boat. Every day, his route takes him 22.5 miles against the current and back to his dock, and he needs to make this trip in a total of 9 hours. he has a boat in mind, but he can only test in on a... show more he speed of the current in a river is 6 mph. A ferry operator who works that part of the river is looking to buy a new boat. Every day, his route takes him 22.5 miles against the current and back to his dock, and he needs to make this trip in a total of 9 hours. he has a boat in mind, but he can only test in on a lake where there is no current. How fast must the boat go on the lake in order for it to serve the ferry operator's needs?
~~~~~~~~~~~~~~~~~~~~~~
Let me reformulate the problem equivalently in more convenient terms.
The round trip of 22.5 miles upstream and the same distance downstream takes 9 hours.
Find the speed of the boat in still water if the current rate is 6 mph.
Solution
Let u be the speed of the boat in still water.
Then the speed of the boat traveling upstream is (u-6) mph,
while the speed traveling downstream is (u+6) mph.
The "time" equation is
 = 9.
Solve for u. For it, multiply both sides by 2*(u-6)*(u+6). You will get
45(u+6) + 45*(u-6) = = 9.
Solve for u. For it, multiply both sides by 2*(u-6)*(u+6). You will get
45(u+6) + 45*(u-6) = 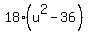 , --->
90u = , --->
90u = 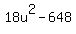 , ,
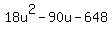 = 0 ---> = 0 --->
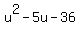 = 0 ---> (u-9)*(u+4) = 0 --->
The only positive root is u = 9.
Answer. The speed of the boat in still water is 9 mph.
Check. = 0 ---> (u-9)*(u+4) = 0 --->
The only positive root is u = 9.
Answer. The speed of the boat in still water is 9 mph.
Check. 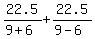 = 9 hours. Correct !! = 9 hours. Correct !!
It is a typical and standard Upstream and Downstream round trip word problem.
You can find many similar fully solved problems on upstream and downstream round trips with detailed solutions in lessons
- Wind and Current problems
- More problems on upstream and downstream round trips
- Selected problems from the archive on the boat floating Upstream and Downstream
in this site.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
|
|
|