|
Question 1070535: Desmond will discharge a debt of R500 000 six years from now, using the sinking fund method. The debtís
interest is 15,6% per year, paid quarterly. The sinking fund will earn interest at a rate of 8,4% per year,
compounded monthly
a)The monthly deposit into the sinking fund will equal
b)The total yearly cost to discharge the debt (to the nearest rand) will equal
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i don't think i've ever done one like this before but i'll give it a shot, based on what i know.
the debt is 500,000 that has to be all paid up in 6 years.
the interest rate on the debt is 15.6 percent per year compounded quarterly.
the quarterly interest rate on the debt is 15.6/4 = 3.95 per quarter.
the number of quarters is equal to 6 * 4 = 24.
the payment on the debt at the end of each quarter is equal to 32,458.53
his sinking fund investment needs to give him 32,458.53 at the end of each quarter.
the sinking fund earns interest at the rate of 8.4 percent per year compounded quarterly.
the monthly interest rate is 8.4 / 12 = .7 percent per month.
this sinking fund needs to provide him with 32,458.53 at the end of each 4 month period.
he will have to put in 8,029.92 at the end of each month.
i used an online calculator at http://arachnoid.com/finance/ to make the required calculations.
the first calculation was to find the quarterly payments required.
the second calculation was to find the monthly depoists required to get the auqarterly payments every 4 months.
following are the results of each calculation.
first is the calculation for determining what the quarterly payments need to be.
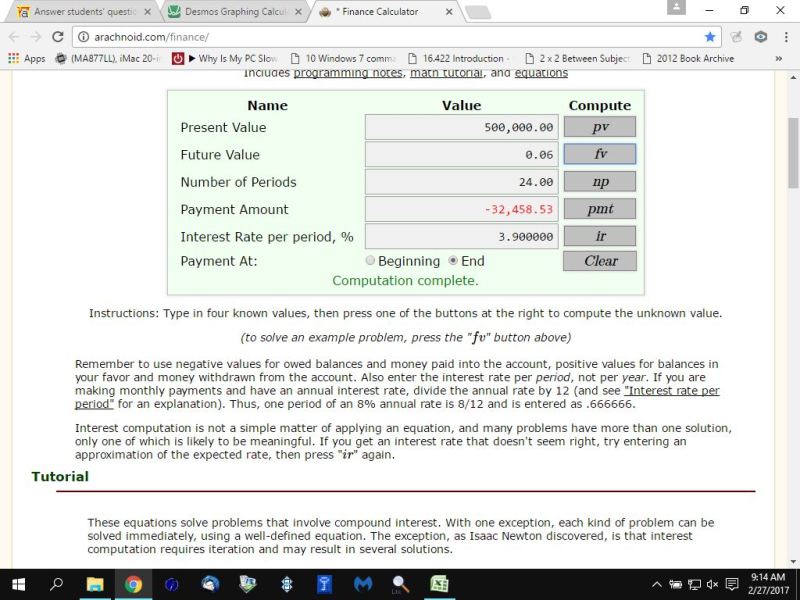
next is the calculation for determining what the monthly deposits need to be.
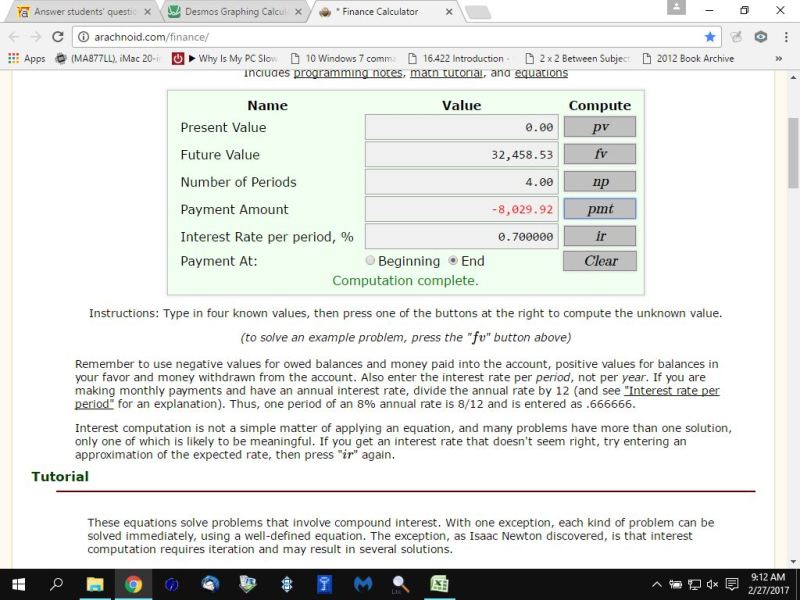
the solution is that he needs to deposit 8,029.92 at the end of each month in order to have the required quarterly payment of 32,458.53 at the end of each quarter.
|
|
|
| |