Question 1070505: A man takes 5 hours and 20 minutes to row 6 miles up a river and back. If he can row 3 miles downstream in the same time that he can row 1 mile upstream, find the rate at which he rows and the rate of the current.
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A man takes 5 hours and 20 minutes to row 6 miles up a river and back. If he can row 3 miles downstream in the same time
that he can row 1 mile upstream, find the rate at which he rows and the rate of the current.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let u be the rate of the boat at still water and v be the current rate (in miles-per-hour).
Then the speed of the boat downstream is (u+v) mph,
while the speed of the boat upstream is (u-v) mph.
Hence, you have these two equations for two unknowns
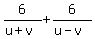 = =   (1) ("A man takes 5 hours and 20 minutes to row 6 miles up a river and back") (1) ("A man takes 5 hours and 20 minutes to row 6 miles up a river and back")
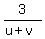 = = 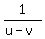 (2) ("he can row 3 miles downstream in the same time that he can row 1 mile upstream")
Simplify equation (1) in this way: (2) ("he can row 3 miles downstream in the same time that he can row 1 mile upstream")
Simplify equation (1) in this way:
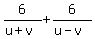 = = 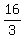 (1')
and replace (1')
and replace 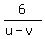 in (1') by in (1') by 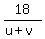 , based on (2). You will get , based on (2). You will get
 = = 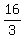 , or , or
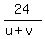 = = 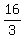 , or (u+v) = , or (u+v) = 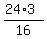 = =  .
Then from (2) u-v = .
Then from (2) u-v = 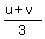 = = 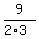 = =  .
You have now this system for u and v:
u + v = .
You have now this system for u and v:
u + v =  , (3)
u - v = , (3)
u - v =  . (4)
Add the two equations. You will get
2u = . (4)
Add the two equations. You will get
2u = 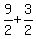 = =  = 6. Hence, u = = 6. Hence, u = 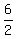 = 3 miles per hour.
Now from (3), v = = 3 miles per hour.
Now from (3), v = 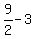 = =  = 1.5 miles per hour.
Answer. The boat speed in still water is 3 miles per hour.
The current speed is 1.5 miles per hour. = 1.5 miles per hour.
Answer. The boat speed in still water is 3 miles per hour.
The current speed is 1.5 miles per hour.
You can find many fully solved problems on upstream and downstream round trips with detailed solutions in lessons
- Wind and Current problems
- More problems on upstream and downstream round trips
- Selected problems from the archive on the boat floating Upstream and Downstream
in this site.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
|
|
|