SOLUTION: Prove that for any integer n, 5 divides n^5-n.

Algebra ->  Proofs -> SOLUTION: Prove that for any integer n, 5 divides n^5-n.      Log On


   

Question 1070422: Prove that for any integer n, 5 divides n^5-n.
Found 2 solutions by solver91311, ikleyn:
Answer by solver91311(24713) About Me  (Show Source):
Answer by ikleyn(52838) About Me  (Show Source):
You can put this solution on YOUR website!
.
Prove that for any integer n, 5 divides n^5-n.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

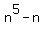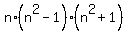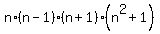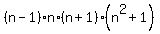n%5E5+-+n = n%2A%28n%5E4-1%29 = n%2A%28n%5E2-1%29%2A%28n%5E2%2B1%29 = n%2A%28n-1%29%2A%28n%2B1%29%2A%28n%5E2%2B1%29 = %28n-1%29%2An%2A%28n%2B1%29%2A%28n%5E2%2B1%29.


If n is a multiple of 5, the statement is true.


If n gives the remainder 1 when divided by 5, then the factor (n-1) is a multiple of 5, and the statement is true.


If n gives the remainder 4 when divided by 5, then the factor (n+1) is a multiple of 5, and the statement is true.


If n gives the remainder 2 when divided by 5, then the factor (n^2+1) is a multiple of 5. 
     Indeed, the remainder of division by 5 is 2%5E2%2B1 = 5 (equivalent to 0) in this case, and the statement is true.


If n gives the remainder 3 when divided by 5, then the factor (n^2+1) is a multiple of 5. 
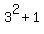     Indeed, the remainder of division by 5 is 3%5E2%2B1 = 10 (equivalent to 0) in this case, and the statement is true.


Thus the statement is true in all cases.

QED.   Proved and solved.