Question 1070274: Prove that the product of two odd numbers is odd, using an indirect proof and a proof by contradiction.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Here are two odd numbers.
2n+1, and 2n-1, for some integer, n.
We believe that (2n+1)(2n-1) will be 'even', and we can simplify the product expression, through multiplication:
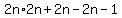
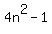
But, is this 'even', or not?
The 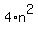 is undoubtedly EVEN. To that is subtracted the ODD number, 1, which together makes 4n^2-1, the product of the two odd numbers, an ODD number.
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
The "proof" by josgarithmetic" is wrong starting from his second line.
The correct proof is this:
Let assume that the product of two odd numbers, m and n, is an even number N: N = m*n.
Then this even number N is a multiple of 2.
The number 2 is a prime number.
Since 2 divides N, it must divide at least one of the factors, n or m.
If 2 divide n, then n is and even number. It contradicts to the original assumption that n is odd.
If 2 divide m, then m is and even number. It contradicts to the original assumption that m is odd.
This/these contradiction/contradictions proves/prove that the product of two odd numbers is an odd number.
QED. Proved and solved.
|
|
|
