Question 1069924: Write a polynomial function of least degree with integral coefficients the zeros of which include -1 and 1 + 2i.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! If your coefficients must be integers (which are real numbers),
the conjugate of every complex zero must also be a zero.
The conjugate of  is  .
The polynomial in  of least degree whose zeros include
 , , and will be
a polynomial of degree  which can be written as
 for some real number  .
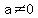We want to work on that to simplify it and show how we can make the coefficients not only real numbers, but also integers.
So far the coefficients in this factored form are
 ,  , and  , which are integers,
so it looks like we can just use  ,
or any non-zero integer we want for  .
Since the coefficients of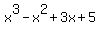 
are the integers , , and ,
the simplest such polynomial, with is
 .
|
|
|
