SOLUTION: Det. Robert Goren is investigating a homicide, and the medical examiner tells him that when he arrived at 6:00 p.m., the body had a temperature of 95.3 degrees Fahrenheit. By the t

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: Det. Robert Goren is investigating a homicide, and the medical examiner tells him that when he arrived at 6:00 p.m., the body had a temperature of 95.3 degrees Fahrenheit. By the t      Log On


   

Question 1069666: Det. Robert Goren is investigating a homicide, and the medical examiner tells him that when he arrived at 6:00 p.m., the body had a temperature of 95.3 degrees Fahrenheit. By the time Nichols had arrived an hour later (at 7:00), he checks again and determines the temperature to be 94.9 degrees. The ambient air temperature is 90 degrees. Use the equation 𝑇(𝑡) = 𝑎𝑒^(−𝑘𝑡) + 90 to determine when the victim was killed. (The normal body temperature is 98.6 degrees. Round k to 3 decimal places and find the time of death to the nearest minute.
I'm really confused on how to go about this problem, any help would be greatly appreciated!
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
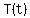T%28t%29=a%2Ae%5E%28-kt%29%2B90 makes some sense.
T%28t%29 would be the body temperature in degrees at some time t.

ONE WAY TO SOLVE:
We define t= time in minutes after 6:00 p.m.;
substitute T%280%29=95.3 and T%2860%29=94.9 to find a and k,
and then use T%28t%29=98.6 to find the time the victim died.
Adding the negative time we find to 6:00 p.m. gives us the murder time.
It gets easier if we solve T%28t%29=a%2Ae%5E%28-kt%29%2B90 for what we want to start,
and then just plug stuff in.
a=%28T-90%29%2Fe%5E%28-kt%29
k=-%281%2Ft%29ln%28%28T-90%29%2Fa%29
t=-%281%2Fk%29ln%28%28T-90%29%2Fa%29
At 6:00 p.m. t=0<-->-kt=0 and T=95.3 , so
a=%2895.3-90%29%2Fe%5E0-->a=5.3%2F1-->highlight%28a=5.3%29
At 7:00 p.m. t=60 and T=94.9 , so
k=-%281%2F60%29ln%28%2894.9-90%29%2F5.3%29-->k=-%281%2F60k%29ln%284.9%2F5.3%29-->k=-%281%2F60%29%28-0.7850%29-->highlight%28k=0.001308%29
At the time the victim died, T=98.6 , so
t=-%281%2F60%29ln%28%2898.6-90%29%2F5.3%29-->t=-%281%2F60%29ln%288.6%2F5.3%29-->t=-%281%2F60%290.4840-->highlight%28t=-370%29 (rounded to the nearest minute)
Since 370minutes=6hours%2B11minutes ,
time of death = %226%3A00+PM%22-%226%3A11%22=highlight%28%2211%3A49+AM%22%29 .

EXPLANATION AND ALTERNATE WAY TO SOLVE:
You may have heard in class that
y=e%5E%28-kx%29 for some k%3E0 , graph%28200%2C200%2C-0.1%2C0.9%2C-0.1%2C0.9%2C0.8%2Ae%5E%28-%28sqrt%285x%29%5E2%29%29%29
models exponential decay;
that it asymptotically approaches y=0,
or even that lim%28x-%3Einfinity%2Ce%5E%28-kx%29%29=0 .

T%28t%29=a%2Ae%5E%28-kt%29%2B90 (with some a%3E0 and k%3E0 too) makes sense.
It would have T%280%29=a%2Ae%5E0%2B90=a%2A1%2B90=a%2B90 ,
and would decrease towards 90 , which is the ambient temperature in degrees.
Nothing else is specified about that function,
so we will say that
t= time since 6:00 p.m., in minutes.
So, T%280%29=95.3 tells us that
a%2B90=95.3 --> a=95.3-90 ---> highlight%28a=5.3%29
An hour later, t=60 ,
and T%2860%29=94.9 tells us that
a%2Ae%5E%28-60k%29%2B90=94.9 --> 5.3%2Ae%5E%28-60k%29=94.9-90 --> 5.3%2Ae%5E%28-60k%29=4.9
--> e%5E%28-60k%29=4.9%2F5.3 --> -60k=ln%280.9245%29 --> -60k=-0.07850
--> k=%28-0.07850%29%2F%28-60%29 --> highlight%28k=0.001308%29
Now we have the function
T%28t%29=5.3e%5E%28-0.001308t%29%2B90
and we want to find t for T%28t%29=98.6
98.6=5.3e%5E%28-0.001308t%29%2B90
98.6-90=5.3e%5E%28-0.001308t%29
8.6=5.3e%5E%28-0.001308t%29
8.6%2F5.3=e%5E%28-0.001308t%29
ln%288.6%2F5.3%29=-0.001308t
t=ln%288.6%2F5.3%29%2F%28-0.001308%29
highlight%28t=-370%29 (rounded to the nearest minute)
Since 370minutes=6hours%2B11minutes ,
time of death = %226%3A00+PM%22-%226%3A11%22=highlight%28%2211%3A49+AM%22%29 .