SOLUTION: cramer rule x+2y+2z=2;x+y+z=0;x-2z=-0.4 solve this math

Write in all the 1 coefficients, as well as +0y
in the third equation for the missing term in y:



Cramer's rule:
 
There are 4 columns,
 
1. The column of x-coefficients 
 
2. The column of y-coefficients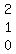 
 
3. The column of z-coefficients  
 
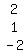4. The column of constants:     
 
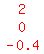There are four determinants:
 
1. The determinant  consists of just the three columns
of x, y, and z coefficients. in that order, but does not
contain the column of constants.
 
. 
 
It has value .  I'm assuming you know how to find the
value of a 3x3 determinant, for that's a subject all by itself.
If you don't know how, ask me for help in the thank-you note
form below. 
 
2. The determinant  is like the determinant 
except that the column of x-coefficients is replaced by the
column of constants.   does not contain the column 
of x-coefficients.
 
.
 
It has value .
 
3. The determinant  is like the determinant 
except that the column of y-coefficients is replaced by the
column of constants.   does not contain the column 
of y-coefficients.
 
.
 
It has value .
 
4. The determinant  is like the determinant 
except that the column of z-coefficients is replaced by the
column of constants.   does not contain the column 
of z-coefficients.
 
.
 
It has value .
 
Now the formulas for x, y and z are
 



 
Solution =  = 

Edwin