We will use the theorem:
If a perfect square is divisible by a prime p,
it is also divisible by p².
Assume that when we divide n²-2 by 4
we get an integer k
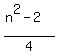
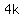
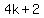
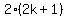Therefore n² is divisible by 2.
Since n² is divisible by 2, and 2 is a prime,
by the theorem n² must be divisible by 2², or 4.
Therefore 2k+1 must be divisible by 2,
but 2k+1 is an odd number and is not divisible
by 2, so we have reached a contradiction.
Therefore the assumption that n²-2 is divisible by 4
is incorrect, and therefore n²-2 is not divisible by 4.
Edwin
