Question 1069261: If the compound interest formula is solved for a, we get
a equals StartFraction y Over left-parenthesis 1 plus n right-parenthesis Superscript t EndFraction
where a is the amount that must be deposited now at interest rate n to produce an amount y in t years. How much money would have to be invested at 7.5% per year to accumulate to $10000 in 13 years?
Round to the nearest dollar.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I agree that with
 = final balance, = final balance,
 = amount initially deposited/invested, = amount initially deposited/invested,
 = annual yield (as a decimal), = annual yield (as a decimal),
 = number of years, = number of years,
the relationship between those variables is
 or or  . .
In this case,  because the yield per year is because the yield per year is

All you have to do is substitute the values for  , ,  , and , and  : :
a =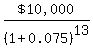 = =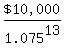 = =
NOTE: The values 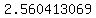 and and 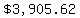 are rounded, are rounded,
and I used help from the computer to calculate the final result,
with the computer doing its best to calculate 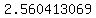 and and 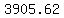 accurately, accurately,
and properly rounding the results for display purposes.
|
|
|